2024年成考高起点《数学(理)》每日一练试题11月26日

2024年成考高起点《数学(理)》每日一练试题11月26日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知直线l：3x-2y-5=0，圆C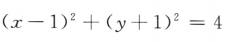：，则C上到l的距离为1的点共有（）

• A：1个
• B：2个
• C：3个
• D：4个

答 案：D

解 析：由题可知圆的圆心为（1，-1），半径为2 ，圆心到直线的距离为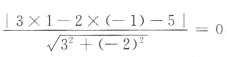,即直线过圆心，因此圆C上到直线的距离为1的点共有4个．

2、设（）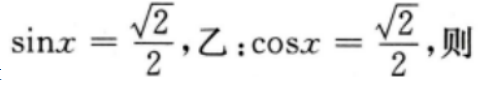

• A：甲是乙的充分条件但不是必要条件
• B：甲是乙的必要条件但不是充分条件
• C：甲是乙的充要条件
• D：甲既不是乙的充分条件也不是乙的必要条件

答 案：D

解 析：本题主要考查的知识点为简易逻辑 由于 故甲既不是乙的充分条件，也不是乙的必要条件

3、“曲线C上的点的坐标都是方程f（x，y）=0的解”是“f（x，y）=0是曲线C的方程”的（）。

• A：充分但非必要条件
• B：必要但非充分条件
• C：充要条件
• D：非充分非必要条件

答 案：B

4、若甲：x>1,乙：则  

• A：甲是乙的必要条件,但不是乙的充分条件
• B：甲是乙的充分必要条件
• C：甲不是乙的充分条件，也不是乙的必要条件
• D：甲是乙的充分条件,但不是乙的必要条件

答 案：D

解 析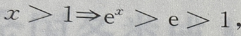：而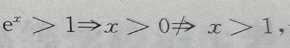故甲是乙的充分条件，但不是必要条件

主观题

1、已知一组数据9.9；10.3；9.8；10.1；10.4；10；9.8；9.7，计算这组数据的方差。  

答 案：

2、建筑一个容积为8000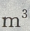,深为6m的长方体蓄水池，池壁每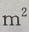的造价为15元，池底每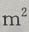的造价为30元。（I）把总造价y(元)表示为长x(m)的函数；（Ⅱ）求函数的定义域  

答 案：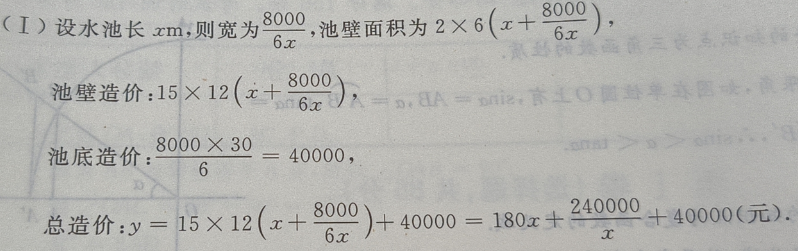

3、求（1+tan10°）（1+tan35°）的值。  

答 案：原式=1+tan10°+tan35°+tan10°·tan35°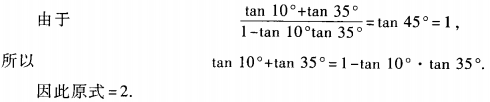

4、求下列函数的最大值、最小值和最小正周期： （1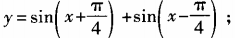）（2）y=6cosx+8sinx

答 案：  

填空题

1、函数的定义域是（）

答 案：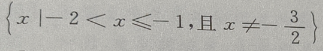

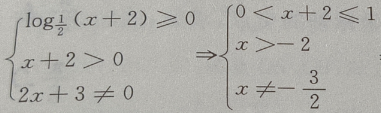
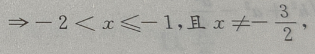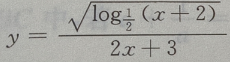解 析：所以函数的定义域是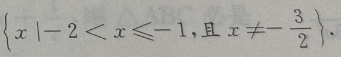

2、已知≤0＜2π，且实数x满足log₃x=2-cos²θ+sin²θ，则x的最小值是______。  

答 案：3

解 析：因为log₃x=2-（cos²θ-sin²θ）=2-cos2θ。 又log₃x中的底数3＞1，因此要使x最小，应使2-cos2θ的值最小，而其最小值为1，故x=3。