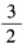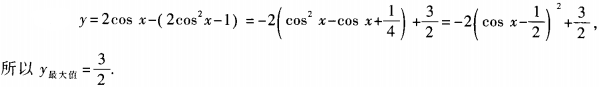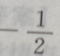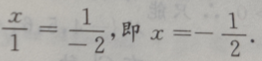课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(理)》每日一练试题11月25日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、某类灯泡使用时数在1000小时以上的概率为0.2,三个灯泡在使用1000小时以后最多只有一个坏的概率为()
答 案:B
解 析:已知灯泡使用1000小时后好的概率为0.2,坏的概率为1-0.2=0.8,则三个灯泡使用1000小时以后,可分别求得: P(没有坏的)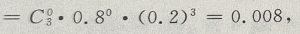 P(一个坏的)
P(一个坏的)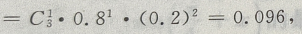 故最多只有一个坏的概率为:0.008+0.096=0.104.
故最多只有一个坏的概率为:0.008+0.096=0.104.
2、函数y=lg(x2-3x+2)的定义域为()。
- A:{x|x<1或x>2}
- B:{x|1<x<2}
- C:{x|x<1}
- D:{x|x>2}
答 案:A
解 析:由x2-3x+2>0,解得x<1或x>2。答案为A。
3、函数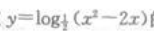 的定义域是()。
的定义域是()。
- A:(-∞,0)∪[2,+∞)
- B:[0,2]
- C:(-∞,0)∪(2,+∞)
- D:(0,2)
答 案:C
解 析:x2-2x>0,解得x<0或x>2.函数的定义域为(-∞,0)∪(2,+∞)。答案为C。
4、抛物线 y=ax2的准线方程是 y=2,则a=()。
- A:
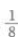
- B:
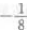
- C:8
- D:-8
答 案:B
解 析: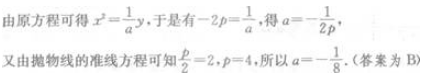
主观题
1、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得 AB=120m,求河的宽
AB=120m,求河的宽

答 案:如图,  ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m
2、cos20°cos40°cos80°的值。
答 案:
3、已知am=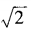 ,an=
,an=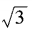 ,求a3n-4m的值。
,求a3n-4m的值。
答 案: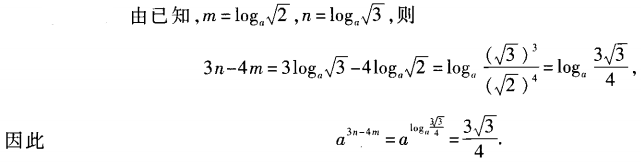
4、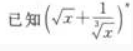 展开式的二项式系数之和比
展开式的二项式系数之和比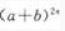 展开式的二项式系数之和小240。 求:(1)
展开式的二项式系数之和小240。 求:(1)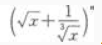 展开式的第3项;
展开式的第3项;
(2)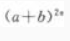 展开式的中间项。
展开式的中间项。
答 案:
填空题
1、函数y=2cosx-cos2x(x∈R)的最大值为______。
答 案: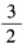
解 析: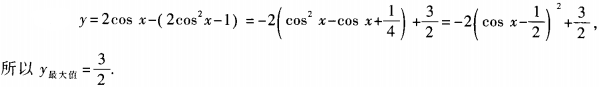
2、若平面向量a=(x,1),b=(1,-2),且a//b,则x=()
答 案: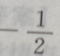
解 析:由于a//b,故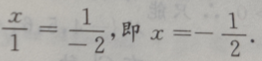
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
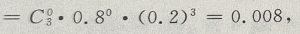 P(一个坏的)
P(一个坏的)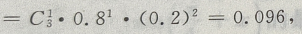 故最多只有一个坏的概率为:0.008+0.096=0.104.
故最多只有一个坏的概率为:0.008+0.096=0.104.
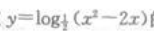 的定义域是()。
的定义域是()。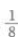
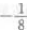
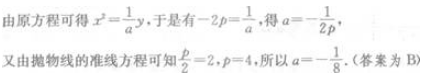
 AB=120m,求河的宽
AB=120m,求河的宽

 ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m

 ,an=
,an=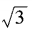 ,求a3n-4m的值。
,求a3n-4m的值。
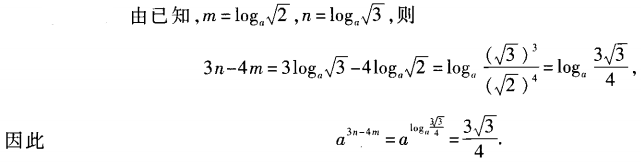
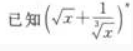 展开式的二项式系数之和比
展开式的二项式系数之和比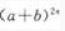 展开式的二项式系数之和小240。 求:(1)
展开式的二项式系数之和小240。 求:(1)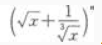 展开式的第3项;
展开式的第3项; 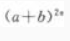 展开式的中间项。
展开式的中间项。