2024年成考高起点《数学(文史)》每日一练试题11月24日
2024-11-24 12:26:15 来源:吉格考试网
2024年成考高起点《数学(文史)》每日一练试题11月24日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、设0<x<1,则()。
- A:1<2x<2
- B:0<2x<1
- C:
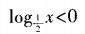
- D:log2x>0
答 案:A
解 析:函数y=2x在区间(-∞,+∞)内为增函数,则2x>20=1,且2x<21=2,选A。
2、函数f(x)=x3-6x2+9x-3的单调区间为()。
- A:(-∞,-3),(-3,1),(1,+∞)
- B:(-∞,-1),(-1,3),(3,+∞)
- C:(-∞,-3),(-3,-1),(-1,+∞)
- D:(-∞,1),(1,3),(3,+∞)
答 案:D
解 析:∵x∈R
f’(x)=3x2-12x+9
=3(x2-4x+3)
=3(x-3)(x-1)
∴x>3或x<1,f’(x)>0,
1 3、已知两数的等差中项为10,等比中项为8,则以这两数为根的一元二次方程是()。 答 案:D 4、从1、2、3、4、5、6、7、8、9这九个数字中,随机取出一个数字,这个数字是奇数的概率是()。
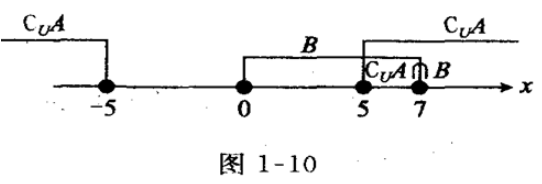
答 案:B 主观题 1、已知x+x-1= 答 案:由已知,得 2、设全集U=R,集合A={x|-5<x<5},B={x|0≤x≤7},求CUA∩B. 答 案:解:全集U=R,A={x|-5<x<5},B={X|0≤x≤7},因为CuA={x|x≤-5或x≥5},所以CuA∩B={x|x≤-5或x≥5}N{x|0≤x≤7}={x|5≤x≤7},如图1—10所示。 3、如图:已知在△ADC中,∠C=90°,∠D=30°,∠ABC=45°,BD=20,求AC(用小数表示,保留一位小数)
答 案:如图 4、设函数f(x) 答 案:(Ⅰ)由已知得f'= 填空题 1、全集U,集合M,N如图1—7所示,用列举法表示M,N,CUM,CUN。 答 案:如图1—7,有M={1,2,3,4,5},N={4,5,6,7,8},CUM={6,7,8,9,10,11},CUN={1,2,3,9,10,11}。 2、已知点P(-3,1)为角α终边上一点,则cos(2α-π)的值等于______。
答 案: 解 析:因为cos(2α-π)=cos(π-2α)=-cos2α。由已知,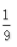
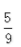
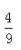
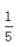
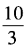 ,求x2+x-2的值。
,求x2+x-2的值。



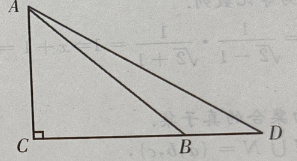
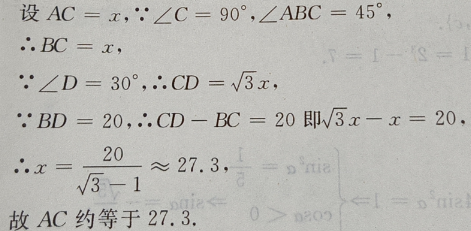
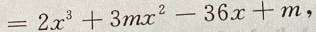 且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间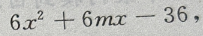 又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=
又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=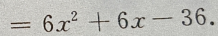 令f'(x)=0,解得
令f'(x)=0,解得 当x<-3时,f'(x)>0;
当-3
当x<-3时,f'(x)>0;
当-3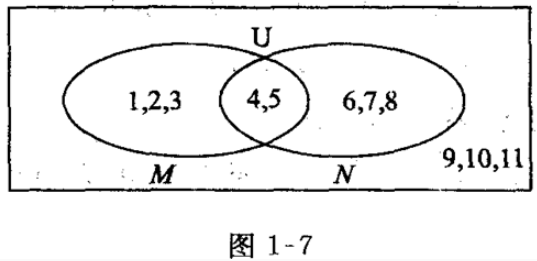
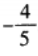
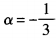 所以
所以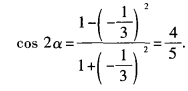
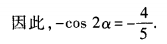
2022年成考高起点《数学(文史)》每日一练试题11月24日 11-24 2023年成考高起点《数学(文史)》每日一练试题11月24日 11-24 2024年成考高起点《数学(文史)》每日一练试题08月24日 08-24 2024年成考高起点《数学(文史)》每日一练试题06月24日 06-24 2024年成考高起点《数学(文史)》每日一练试题07月24日 07-24 2024年成考高起点《数学(文史)》每日一练试题05月24日 05-24 2024年成考高起点《数学(文史)》每日一练试题01月24日 01-24 2024年成考高起点《数学(文史)》每日一练试题02月24日 02-24



