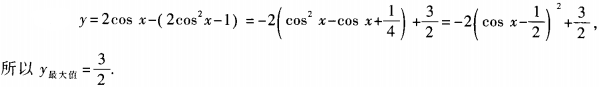2024年成考高起点《数学(理)》每日一练试题11月22日

2024年成考高起点《数学(理)》每日一练试题11月22日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、下列关系式中，对任意实数A＜B＜0都成立的是（）。

• A：a²＜b²
• B：lg(b－a)＞0
• C：2^a＜2^b
• D：lg(-a)＜lg(－b)

答 案：C

2、与1775°的终边相同的绝对值最小的角是（）。

• A：335°
• B：-25°
• C：25°
• D：155°

答 案：B

解 析：1775°=5×360°+（-25°），故所求角为-25°。  

3、抛物线 y=ax²的准线方程是 y=2,则a=（）。

• A：
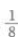
• B：
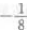
• C：8
• D：－8

答 案：B

解 析：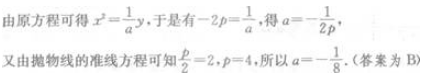

4、设f(x)是以7为周期的偶函数，且f(-2)＝5，则f(9)＝（）。

• A：-5
• B：5
• C：-10
• D：10

答 案：B

解 析：因为f(x)是偶函数，所以f(2)＝f(-2)＝5，又因为f(x)是以7为周期的函数，则f(9)＝f(7＋2)＝f(2)＝5。答案为B。

主观题

1、设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．

答 案：(I）f(1)=1,f'(x)=2+lnx，故f'(1)=2.所以曲线y=f(x）在点（1,f(1))处的切线方程为y=2x-1.(II）令f'(x)=0，解得当时，f'(x)时，f'(x)＞O.故f(x）在区间单调递减，在区间单调递增．因此f(x）在时取得极小值

2、空间有四个点，如果其中任何三点不在同一直线上，可以确定几个平面?  

答 案：根据公理，在所给定的四点中任取三点，可确定一个平面，由组合公式所以共可确定四个平面。

解 析：空间有n个点，如果其中任何三点不在同一直线上，可以确定个平面。  

3、已知log₅3=a，log₅4=b，求log₂₅12关于a，b的表达式。  

答 案：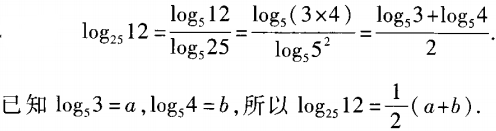

4、求下列函数的最大值、最小值和最小正周期： （1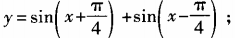）（2）y=6cosx+8sinx

答 案：  

填空题

1、sin²10°+sin²20°+sin²40°+sin²50°+sin²70°+sin²80=______。

答 案：3

解 析：由互为余角的余函数值相等得 原式=(sin²10°+cos²10°)+(sin²20°+cos²20°)+(sin²40+cos²40)=1+1+1=3

2、函数y=2cosx-cos2x（x∈R）的最大值为______。  

答 案：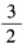

解 析：