课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(文史)》每日一练试题11月20日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、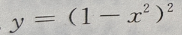 的导数是
的导数是
答 案:C
解 析: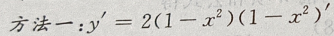
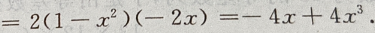
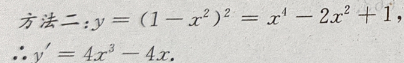
2、甲坛有8个小球,乙坛有4个小球,所有小球颜色各不相同,现从甲坛中取2个小球,乙坛中取1个小球,则取出3个球的不同取法共有()。
答 案:B
解 析:C8(2)×C4(1)=112(种)。
3、设f(x)=1-f(x)log2x函数,则f(2)=()
答 案:D
解 析:在f(x)=1-flog2x中令x=2得,f(2)=1-f(2)log22→f(2)=1-f(2)→1/2
4、盒中有20节电池,其中有2节是废品,现从中取3节,其中至少有一节废品的概率是()。
答 案:A
主观题
1、已知x+x-1=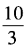 ,求x2+x-2的值。
,求x2+x-2的值。
答 案:由已知,得

2、设全集U=R,集合A={x|-5<x<5},B={x|0≤x≤7},求CUA∩B.
答 案:解:全集U=R,A={x|-5<x<5},B={X|0≤x≤7},因为CuA={x|x≤-5或x≥5},所以CuA∩B={x|x≤-5或x≥5}N{x|0≤x≤7}={x|5≤x≤7},如图1—10所示。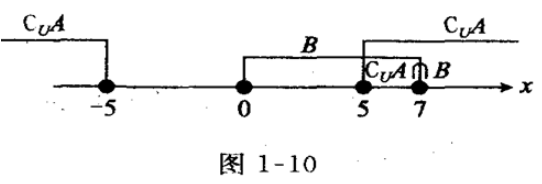
3、设函数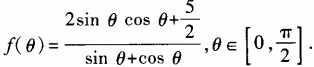 (1)求
(1)求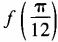 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
答 案:
4、若双曲线 的两条准线将两个焦点的连线分成三等分,求双曲线的离心率。
的两条准线将两个焦点的连线分成三等分,求双曲线的离心率。
答 案:设双曲线的半焦距为c,则双曲线 【考点指要】本题要求根据双曲线的焦距、离心率、准线方程三者之间的关系进行计算,属较容易题,在成人高考中常见.
【考点指要】本题要求根据双曲线的焦距、离心率、准线方程三者之间的关系进行计算,属较容易题,在成人高考中常见.
填空题
1、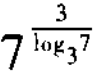 =______。
=______。
答 案:27
解 析: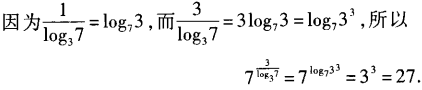
2、与已知直线7x+24y-5=0平行,且距离等于3的直线方程是______。
答 案:7x+24y+70=0或7x+24y-80=0
解 析:设要求的直线方程为7x+24y+c=0, ∵直线7x+24y+c=0到直线7x+24y-5=0的距离等于3
∴ ∴.C=70或-80.
故所求的直线方程为7x+24y+70=0或7x+24y-80=0
∴.C=70或-80.
故所求的直线方程为7x+24y+70=0或7x+24y-80=0
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
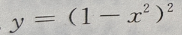 的导数是
的导数是
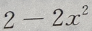
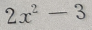


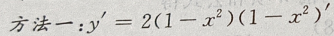
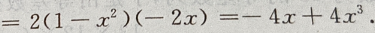
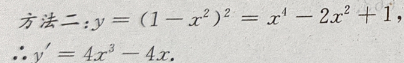
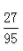
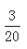
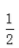
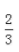
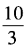 ,求x2+x-2的值。
,求x2+x-2的值。



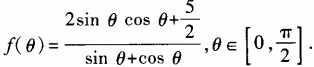 (1)求
(1)求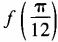 ;(2)求函数f(θ)最小值。
;(2)求函数f(θ)最小值。
 的两条准线将两个焦点的连线分成三等分,求双曲线的离心率。
的两条准线将两个焦点的连线分成三等分,求双曲线的离心率。 【考点指要】本题要求根据双曲线的焦距、离心率、准线方程三者之间的关系进行计算,属较容易题,在成人
【考点指要】本题要求根据双曲线的焦距、离心率、准线方程三者之间的关系进行计算,属较容易题,在成人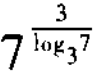 =______。
=______。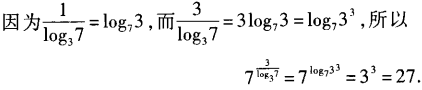
 ∴.C=70或-80.
故所求的直线方程为7x+24y+70=0或7x+24y-80=0
∴.C=70或-80.
故所求的直线方程为7x+24y+70=0或7x+24y-80=0


