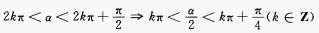课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(理)》每日一练试题11月20日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知tanα,tanβ是方程2x2-4x+1=0的两根,则tan(α+β)=()。
- A:4
- B:-4
- C:
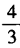
- D:8
答 案:A
解 析:由已知,得tanα+tanβ= =2,tanαtanβ=
=2,tanαtanβ= ,所以
,所以 
2、过A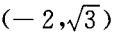 B(-5,0)两点直线的倾斜角为()。
B(-5,0)两点直线的倾斜角为()。
答 案:C
解 析: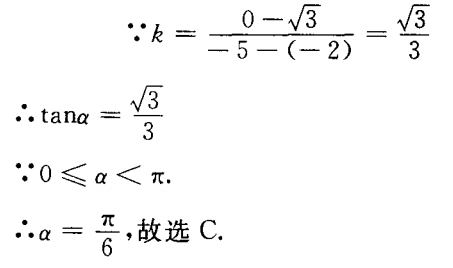
3、若tan(π-α)>0,且cosα>0,则α的终边在()。
答 案:D
解 析:∵tan(π-α)>0 -tanα>0
-tanα>0 tanα<0,且cosα>0∴α在第四象限。
tanα<0,且cosα>0∴α在第四象限。
4、函数y=lg(x2-3x+2)的定义域为()。
- A:{x|x<1或x>2}
- B:{x|1<x<2}
- C:{x|x<1}
- D:{x|x>2}
答 案:A
解 析:由x2-3x+2>0,解得x<1或x>2。答案为A。
主观题
1、空间有四个点,如果其中任何三点不在同一直线上,可以确定几个平面?
答 案:根据公理,在所给定的四点中任取三点,可确定一个平面,由组合公式 所以共可确定四个平面。
所以共可确定四个平面。
解 析:空间有n个点,如果其中任何三点不在同一直线上,可以确定 个平面。
个平面。
2、某气象预报站天气预报的准确率为80%,计算(1)5次预报中恰有4次准确的概率; (2)5次中至少有次准确的概率.(计算结果保留两个有效数字).
答 案: 把每次预报看做一次试验,“预报结果准确”看成事件P(A)=0.8,本题就相当于在5次独立重复试验中求A恰好发生4次(或至少4次)的概率,此题属于独立重复试验,由公式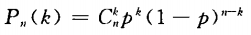 来求解。 (1)n=5;p=0.8;k=4
来求解。 (1)n=5;p=0.8;k=4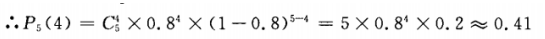 即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即
即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即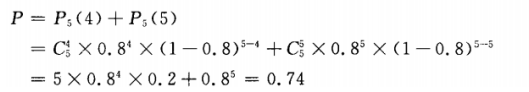 即至少有4次准确的概率为0.74。
即至少有4次准确的概率为0.74。
3、求函数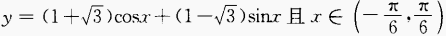 上的最大值以及取得这个最大值的x。
上的最大值以及取得这个最大值的x。
答 案:.1 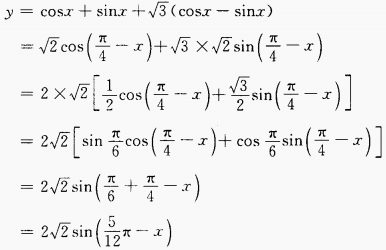
 函数取最大值,即y最大值=。
函数取最大值,即y最大值=。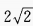
4、设 分别讨论x→0及x→1时f(x)的极限是否存在?
分别讨论x→0及x→1时f(x)的极限是否存在?
答 案: ∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
填空题
1、一个问题在1小时内,甲能独立解决的概率是0.5,乙能独立解决的概率是0.4,两人在1小时内解决问题的概率是______。
答 案:0.7
解 析:设事件A为两人在1小时内解决问题,即1小时内至少有一人能解决问题,事件B为甲在1小时内解决问题,事件C为乙在1小时内解决问题,事件B、C是相互独立事件,事件A的对立事件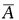 互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(
互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(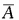 )=1-P(
)=1-P(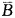 ·
·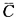 )=1-P(
)=1-P(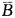 )·P(
)·P(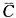 )
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
)
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
2、设a是第一象限角,则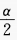 是第______象限角,2α是第______象限角。
是第______象限角,2α是第______象限角。
答 案: 一、三,一、二
解 析: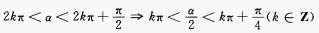

温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
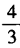
 =2,tanαtanβ=
=2,tanαtanβ= ,所以
,所以 
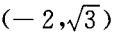 B(-5,0)两点直线的倾斜角为()。
B(-5,0)两点直线的倾斜角为()。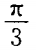
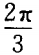
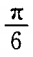
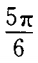
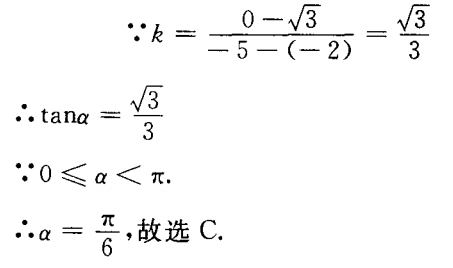
 -tanα>0
-tanα>0 tanα<0,且cosα>0∴α在第四象限。
tanα<0,且cosα>0∴α在第四象限。
 所以共可确定四个平面。
所以共可确定四个平面。 个平面。
个平面。
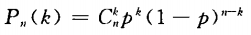 来求解。 (1)n=5;p=0.8;k=4
来求解。 (1)n=5;p=0.8;k=4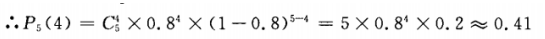 即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即
即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即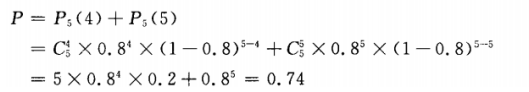 即至少有4次准确的概率为0.74。
即至少有4次准确的概率为0.74。
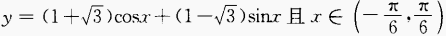 上的最大值以及取得这个最大值的x。
上的最大值以及取得这个最大值的x。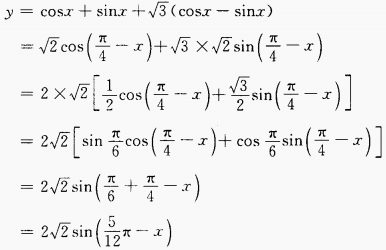
 函数取最大值,即y最大值=。
函数取最大值,即y最大值=。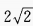
 分别讨论x→0及x→1时f(x)的极限是否存在?
分别讨论x→0及x→1时f(x)的极限是否存在? ∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在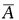 互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(
互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(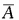 )=1-P(
)=1-P(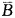 ·
·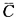 )=1-P(
)=1-P(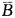 )·P(
)·P(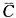 )
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
)
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7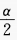 是第______象限角,2α是第______象限角。
是第______象限角,2α是第______象限角。