2024年成考高起点《数学(文史)》每日一练试题11月17日
2024-11-17 12:19:44 来源:吉格考试网
2024年成考高起点《数学(文史)》每日一练试题11月17日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、一枚硬币连抛3次,至少有两次正面向上的概率是()。
- A:
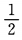
- B:
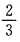
- C:
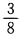
- D:
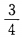
答 案:A
解 析:此题一枚硬币连抛3次等价于3枚硬币抛一次,这种试验的等可能结果总数n=8,其至少两次正面向上的结果总数m=4,故所求概率为 ,故应选A。
,故应选A。
2、不等式|3x+1|≤2的解集是( )
- A:
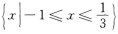
- B:
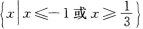
- C:
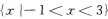
- D:
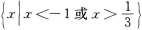
答 案:A
解 析:不等式|3x+1|≤2的解集是不等式3x+1≤2与3x+1≥-2的解集的交集,因此原不等式可写成-2≤3x+1≤2,即-3≤3x≤1,-1≤x≤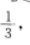 在用集合表示x的解集为
在用集合表示x的解集为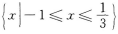 【考点指要】本题主要考查绝对值不等式的解法以及会用集合表示不等式的解集,此类题是成人高考常出现的题型.
【考点指要】本题主要考查绝对值不等式的解法以及会用集合表示不等式的解集,此类题是成人高考常出现的题型.
3、设f(x)=x3+4x2+11x+7,则f(x+1)=()。
- A:x3+7x2+22x+23
- B:x3—7x2+22x+23
- C:x3+7x2-22x+23
- D:x3-7x2-22x+23
答 案:A
解 析:f(x+1) =(x+1)3 +4(x+1}2+11(x+1)+7 =x3+3x2+3x+1+4x2+8x+4+11x+11+7 =x3+7x2+22x+23 综上所述,答案:x3+7x2+22x+23
4、已知向量|a|=3,|b|=4,且a和b的夹角为120°,则a·b=()。
- A:
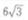
- B:
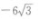
- C:6
- D:-6
答 案:D
主观题
1、教室里有50人在开会,其中学生35人,家长12人,老师3人,现校长在门外听到有人在发言,那么发言人是老师或学生的概率为多少?
答 案:此题属于互斥事件,发言人是老师的概率为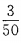 ,是学生的概率为
,是学生的概率为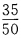 ,故所求概率为。
,故所求概率为。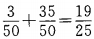
2、设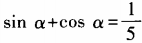 (0<α<π),求tanα的值。
(0<α<π),求tanα的值。
答 案:
3、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.
答 案: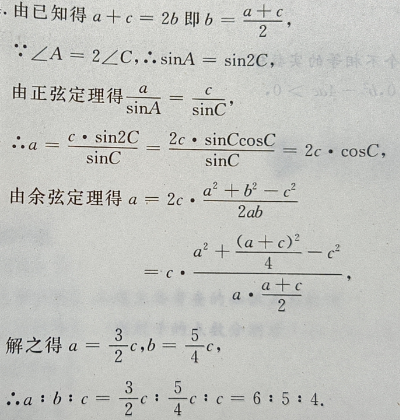
4、已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。
答 案:由已知,得 
填空题
1、函数y=2x(x+1)在x=2处的切线方程是__________.
答 案:10x-y-8=0
解 析:由函数y=2x(x+1) 知,y´=(2x2+2x)'=4x+2,则y´|x=2=10.又当x=2时,y=12,知此函数的切线过点(2,12),且斜率为10。则其切线方程为10(x-2)=y-12,即10x-y-8=0. 【考点指要】本题考查利用导数求曲线的切线方程,y=ƒ(x)在点P(x0,y0)处的导数值即为曲线y=ƒ(x)在该点处切线的斜率.
2、袋中装有3个白球,2个红球,从中任取2个球,取到2个都是红球的概率是______。
答 案:
解 析: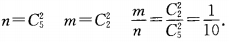
2023年成考高起点《数学(文史)》每日一练试题11月17日 11-17 2022年成考高起点《数学(文史)》每日一练试题11月17日 11-17 2024年成考高起点《数学(文史)》每日一练试题02月17日 02-17 2024年成考高起点《数学(文史)》每日一练试题01月17日 01-17 2024年成考高起点《数学(文史)》每日一练试题05月17日 05-17 2024年成考高起点《数学(文史)》每日一练试题04月17日 04-17 2024年成考高起点《数学(文史)》每日一练试题03月17日 03-17 2024年成考高起点《数学(文史)》每日一练试题06月17日 06-17



