课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(理)》每日一练试题11月11日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、若向量a=(1,-1),b=(1,x),且|a+b|=2,则x=()。
答 案:C
解 析: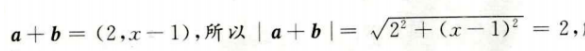 解得x=1 本题主要考查的知识点为向量的加法和模。
解得x=1 本题主要考查的知识点为向量的加法和模。
2、设甲:二次不等式x2+px+q>0的解集为空集合;乙:△=p2-4q<0则()。
- A:甲是乙的必要条件,但不是乙的充分条件
- B:甲是乙的充分条件,但不是乙的必要条件
- C:甲不是乙的充分条件,也不是乙的必要条件
- D:甲是乙的充分必要条件
答 案:D
解 析:由于二次不等式x2+px+q>0的解集为空集合△=p2-4q<0,则甲是乙的充分必要条件(答案为 D)
3、从点M(x,3)向圆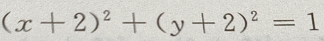 作切线,切线的最小值等于()
作切线,切线的最小值等于()
- A:4
- B:
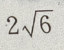
- C:5
- D:
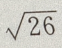
答 案:B
解 析:如图,相切是直线与圆的位置关系中的一种,此题利用圆心坐标、半径,求出切线长. 由圆的方程知,圆心为B(-2,-2),半径为1,设切点为A,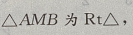 由勾股定理得,
由勾股定理得,
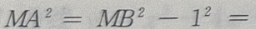

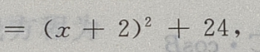
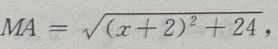 当x+2=0时,MA取最小值,最小值为
当x+2=0时,MA取最小值,最小值为

4、设函数f(x)=logax,且f(4)=2,则下列各式成立的是()。
- A:f(3)<O
- B:
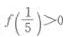
- C:f(5)<f(3)
- D:f(3)<f(5)
答 案:D
解 析:由f(4)-loga4=2,得a2=4,又a>0,故a=2,对于函数f(x)=logax,根据对数函数的性质有f(5)>f(3)成立.(答案为 D)
主观题
1、已知关于x的二次方程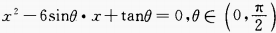 的两根相等,求sinθ+cosθ的值。
的两根相等,求sinθ+cosθ的值。
答 案:

2、计算。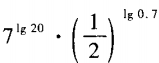
答 案: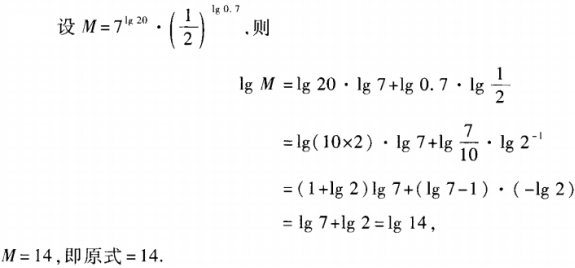
3、已知A(1,4),B(3,8),C(4,10)。求证A、B、C三点共线。
答 案: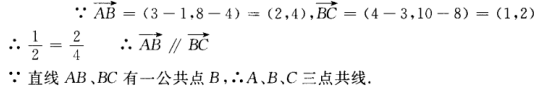
4、某工厂每月生产x台游戏机的收入为R(x)= +130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
+130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
答 案:利润 =收入-成本, L(x)=R(x)-C(x)= +130x-206-(50x+100)=
+130x-206-(50x+100)=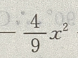 +80x-306
法一:用二次函数
+80x-306
法一:用二次函数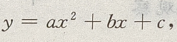 当a<0时有最大值
当a<0时有最大值
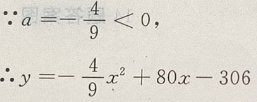 是开口向下的抛物线,有最大值
是开口向下的抛物线,有最大值
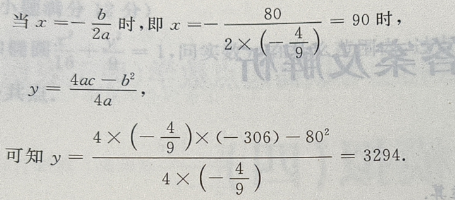 法二:用导数来求解
法二:用导数来求解
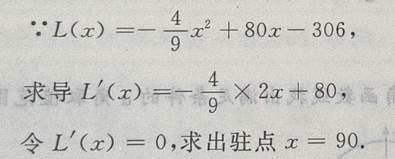 因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
填空题
1、已知≤0<2π,且实数x满足log3x=2-cos2θ+sin2θ,则x的最小值是______。
答 案:3
解 析:因为log3x=2-(cos2θ-sin2θ)=2-cos2θ。 又log3x中的底数3>1,因此要使x最小,应使2-cos2θ的值最小,而其最小值为1,故x=3。
2、sin210°+sin220°+sin240°+sin250°+sin270°+sin280=______。
答 案:3
解 析:由互为余角的余函数值相等得
原式=(sin210°+cos210°)+(sin220°+cos220°)+(sin240+cos240)=1+1+1=3
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
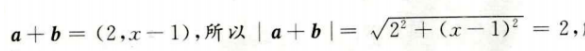 解得x=1 本题主要考查的知识点为向量的加法和模。
解得x=1 本题主要考查的知识点为向量的加法和模。 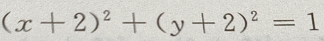 作切线,切线的最小值等于()
作切线,切线的最小值等于()
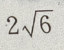
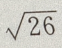
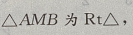 由勾股定理得,
由勾股定理得,
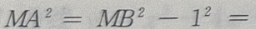

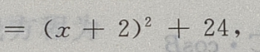
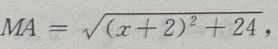 当x+2=0时,MA取最小值,最小值为
当x+2=0时,MA取最小值,最小值为

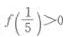
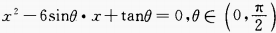 的两根相等,求sinθ+cosθ的值。
的两根相等,求sinθ+cosθ的值。

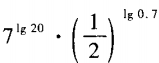
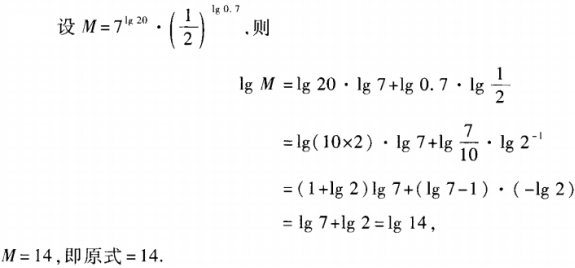
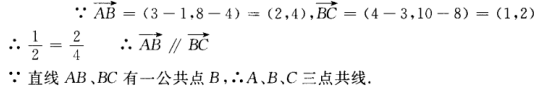
 +130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
+130x-206(百元),成本函数为C(x)=50x+100(百元),当每月生产多少台时,获利润最大?最大利润为多少?
 +130x-206-(50x+100)=
+130x-206-(50x+100)=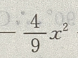 +80x-306
法一:用二次函数
+80x-306
法一:用二次函数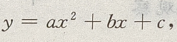 当a<0时有最大值
当a<0时有最大值
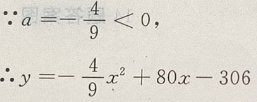 是开口向下的抛物线,有最大值
是开口向下的抛物线,有最大值
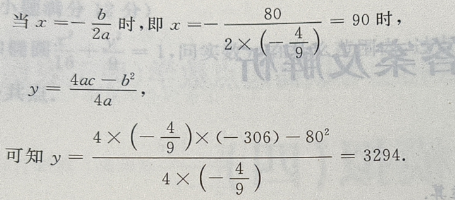 法二:用导数来求解
法二:用导数来求解
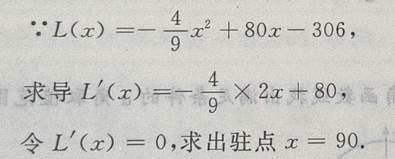 因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294
因为x=90是函数在定义域内唯一驻点
所以x=90是函数的极大值点,也是函数的最大值点,其最大值为L(90)=3294



