课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(文史)》每日一练试题11月10日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、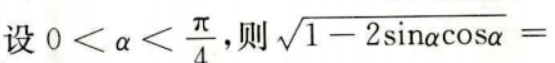 ()。
()。
- A:sinα+cosα
- B:-sinα—cosα
- C:sinα—cosα
- D:cosα—sinα
答 案:D
解 析:本题主要考查的知识点为三角函数的运算。 当时,cosα>sinα>0,所以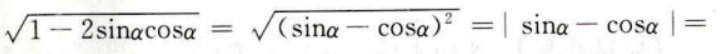
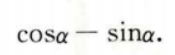
2、数列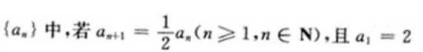 则前5项的和是()。
则前5项的和是()。
- A:-31/8
- B:31/32
- C:-31/32
- D:31/8
答 案:D
解 析:
3、直线 绕原点按逆时针方向旋转30°后所得直线与圆(x-2)2+y2=3的位置关系是()。
绕原点按逆时针方向旋转30°后所得直线与圆(x-2)2+y2=3的位置关系是()。
- A:直线过圆心
- B:直线与圆相交,但不过圆心
- C:直线与圆相切
- D:直线与圆相离
答 案:C
4、下列各等式不成立的是()。
- A:3x·2x=6x
- B:9x=(3x)2
- C:
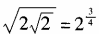
- D:
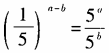
答 案:D
解 析:3x·2x=(3·2)x=6x,排除A;(3x)2=(32)x=9x,排除B
 ,排除C。选D。
,排除C。选D。
主观题
1、求证:双曲线的一个焦点到一条渐近线的距离等于虚半轴的长.
答 案:设双曲线的方程为 则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为
则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为 令设焦点F2(c,0)到渐近线
令设焦点F2(c,0)到渐近线 的距离为d,则
的距离为d,则 即从双曲线
即从双曲线 的一个焦点F2(c,0)到一条渐近线
的一个焦点F2(c,0)到一条渐近线 的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线
的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线 以及点F1(-c,0)到渐近线
以及点F1(-c,0)到渐近线 的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
解 析:本题考查的是圆锥曲线与直线位置关系的推理能力,主要是用代数的方法表示几何中的问题.考生必须对曲线方程、几何性质及元素之间的关系有深刻的理解,方可解决此类综合题.这种综合性的圆锥曲线试题出现的概率比较高,要引起重视.
2、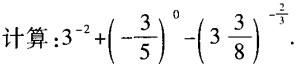
答 案:
3、已知x+x-1=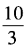 ,求x2+x-2的值。
,求x2+x-2的值。
答 案:由已知,得

4、一艘渔船在航行中遇险,发出警报,在遇险地点西南10海里处有一艘货轮,接收到报时,发现遇险渔船正以9海里/小时的速度与沿南偏东75°方向向某小岛靠近,如果要在40分内将这艘渔船救出,求货轮航行的方向和速度。
答 案:货轮沿东偏北21.8°的方向,以21海里/小时的船速航行。
填空题
1、已知tanθ=1/2,则sin2θ+sin2θ=__________.
答 案:1
解 析:
2、全集U,集合M,N如图1—7所示,用列举法表示M,N,CUM,CUN。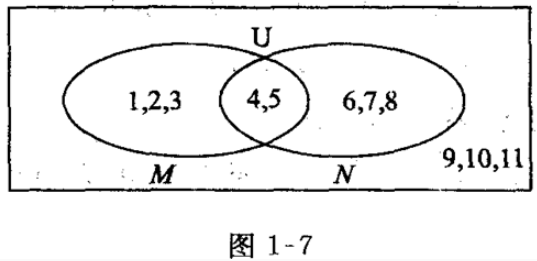
答 案:如图1—7,有M={1,2,3,4,5},N={4,5,6,7,8},CUM={6,7,8,9,10,11},CUN={1,2,3,9,10,11}。
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
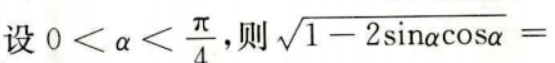 ()。
()。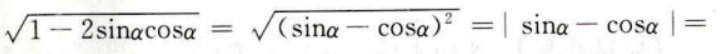
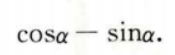
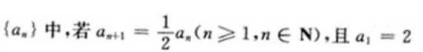 则前5项的和是()。
则前5项的和是()。
 绕原点按逆时针方向旋转30°后所得直线与圆(x-2)2+y2=3的位置关系是()。
绕原点按逆时针方向旋转30°后所得直线与圆(x-2)2+y2=3的位置关系是()。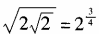
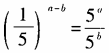

 ,排除C。选D。
,排除C。选D。 则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为
则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为 令设焦点F2(c,0)到渐近线
令设焦点F2(c,0)到渐近线 的距离为d,则
的距离为d,则 即从双曲线
即从双曲线 的一个焦点F2(c,0)到一条渐近线
的一个焦点F2(c,0)到一条渐近线 的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线
的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线 以及点F1(-c,0)到渐近线
以及点F1(-c,0)到渐近线 的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.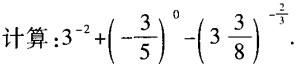

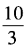 ,求x2+x-2的值。
,求x2+x-2的值。







