2024年成考高起点《数学(理)》每日一练试题11月04日

2024年成考高起点《数学(理)》每日一练试题11月04日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知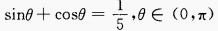，则cotθ的值是（）。

• A：
• B：
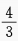
• C：
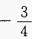
• D：

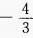
答 案：C

解 析：从已知式两边平方得到，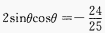

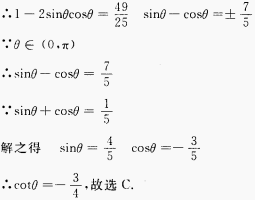
2、5名高中毕业生报考3所院校,每人只能报一所院校,则有（）种不同的报名方法  

• A：
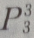
• B：
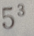
• C：
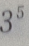
• D：

答 案：C

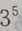解 析：将院校看成元素,高中生看成位置,由重复排列的元素、位置的条件口诀: “元素可挑剩，位置不可缺”，重复排列的种数共有种,即将元素的个数作为底数,位置的个数作为指数.即:元素(院校)的个数为 3,位置(高中生)的个数为5,共有种。  

3、设f(x)是以7为周期的偶函数，且f(-2)＝5，则f(9)＝（）。

• A：-5
• B：5
• C：-10
• D：10

答 案：B

解 析：因为f(x)是偶函数，所以f(2)＝f(-2)＝5，又因为f(x)是以7为周期的函数，则f(9)＝f(7＋2)＝f(2)＝5。答案为B。

4、若tan(π-α)＞0，且cosα＞0，则α的终边在（）。

• A：第一象限
• B：第二象限
• C：第三象限
• D：第四象限

答 案：D

解 析：∵tan(π-α)＞0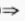-tanα＞0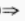tanα＜0,且cosα＞0∴α在第四象限。  

主观题

1、已知tan²θ=2tan²ψ+1，求cos2θ+sin²ψ的值。

答 案：由已知，得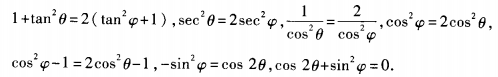

2、已知A（1，4），B（3，8），C（4，10）。求证A、B、C三点共线。  

答 案：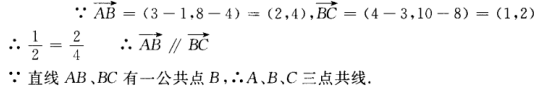

3、已知数列的前n项和 求证：是等差数列，并求公差和首项。  

答 案：  

4、已知数列{a_n}中，a₁=2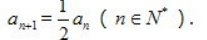， （Ⅰ）求数列{a_n}的通项公式; （Ⅱ）求数列{a_n}前5项的和 S₅

答 案：解：

填空题

1、若P（3，2）是连接P1（2，y）和P2（x，6）线段的中点，则x=______，y=______。  

答 案：x=4，y=-2  

解 析：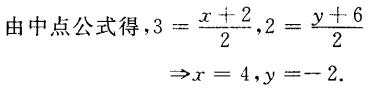

2、已知sin²θ+1=cos²θ，则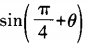的值等于______。  

答 案：

解 析：由已知，cos²θ-sin²θ=1，即cos²θ-（1-cos²θ）=1，cos²θ=1，所以cosθ=±1。 而当cosθ=±1时，sinθ=0。