2024年成考高起点《数学(理)》每日一练试题10月30日
2024-10-30 12:07:07 来源：吉格考试网
2024年成考高起点《数学(理)》每日一练试题10月30日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、圆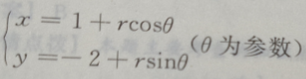
的圆心在（）点上
- A：(1,-2)
- B：(0,5)
- C：(5,5)
- D：(0,0)
答 案：A
解 析：因为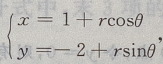
所以圆的圆心为O（1，-2）
2、命题甲：lgx，lgy，lgz成等差数列；命题乙：y2＝x·z则甲是乙的（）。
- A：充分而非必要条件
- B：必要而非充分条件
- C：既充分又必要条件
- D：既非充分也非必要条件
答 案：A
3、已知{i，j，k}是单位正交基底，a＝i＋j，b＝－i＋j－k，则a·b＝（）。
- A：-1
- B：1
- C：0
- D：2
答 案：C
解 析：a·b＝（1，1，0）·（－1，1，－1）＝1×（－1）＋1×1＋0×（－1）＝0。答案为C。
4、函数y=sinx+cosx（x∈R）的最小正周期为（）。
- A：2π
- B：π
- C：
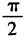
- D：
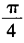
答 案：A
解 析：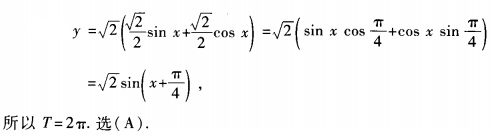
主观题
1、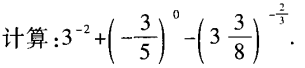
答 案：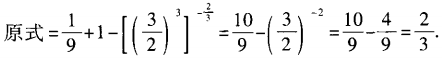
2、已知数列{an}中，a1=2，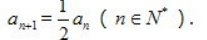
（Ⅰ）求数列{an}的通项公式;
（Ⅱ）求数列{an}前5项的和 S5
答 案：解：
3、设A1A2A3A4A5A6为正六边形，如图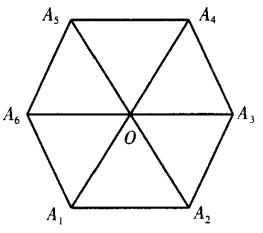
，O为它的中心。 （1）求证： 
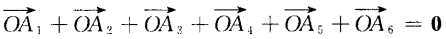（2）
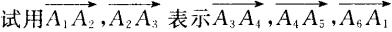
答 案：已知A1A2A3A4A5A6 为正六边形，即|A1A2|=|A3A4|=......|A6A1|.要证6个向量的和为0.只需证其中3个向量与另3个向量的长度相等、方向相反即可.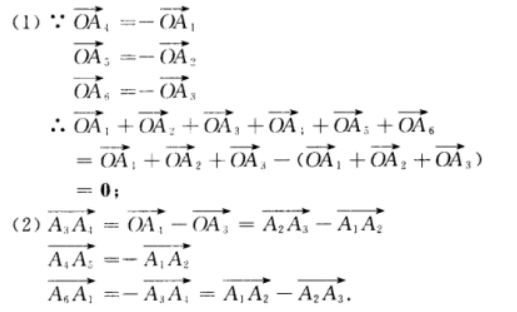
4、已知x+x-1=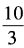
，求x2+x-2的值。
答 案：由已知，得
填空题
1、在自然数1、2、…、100中任取一个数，该数能被3整除的概率是______。
答 案：0.33
解 析：此题随机试验包含的基本事件总数n=100，且每个数能被取到的机会均等，即属于等可能事件的概率能被3整除的自然数的个数m=33，故所求概率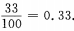
2、函数
的定义域是（）
答 案：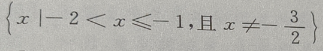
解 析：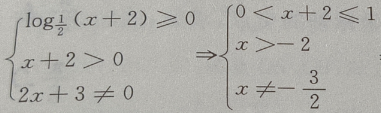
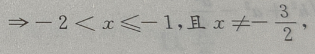所以函数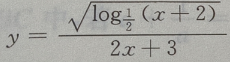
的定义域是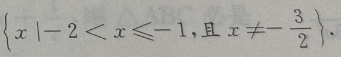
温馨提示：因考试政策、内容不断变化与调整，本站提供的以上信息仅供参考，如有异议，请考生以权威部门公布的内容为准！
- 备考交流
-
2024成考内部交流群群号：665429327
扫一扫或点击二维码入群
热门资讯
相关试卷
猜你喜欢
换一换
成人高考加分条件有哪些 成考怎么进行加分
01-26
张家界航空工业职业技术学院2024年单招二志愿考试安排
04-09
长沙幼儿师范高等专科学校2024年单招二志愿缴费操作说明
04-09
湖南外国语职业学院2024年单招第二志愿考试安排
04-08
怀化师范高等专科学校2024年单招第二志愿考试时间安排
04-08
湖南软件职业技术大学2024单招第二志愿考生考试安排及缴费、准考证打印说明
04-08
张家界航空工业职业技术学院2024年单招二志愿计划安排
03-27
湖南有色金属职业技术学院2024年单独各专业录取分数线
03-26
