课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(理)》每日一练试题10月29日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、若a>b>0,则()。
- A:log2a
- B:2a<2b
- C:
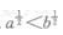
- D:
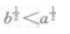
答 案:D
解 析:根据指数函数与对数函数的单调性可知,当a>b>0时,有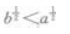 恒成立
恒成立
2、函数F(x)=f(x)·sinx是奇函数,则f(x)()。
- A:是偶函数
- B:是奇函数
- C:既是偶函数又是奇函数
- D:既不是偶函数又不是奇函数
答 案:A
解 析:因为函数F(x)=f(x)·sinx是奇函数,sinx是奇函数, 故 F(-x)=-F(x),sin(-xx)=-sinx.
即f(x)sin(-x)=-f(x)sinx,得f(x)=f(-x),则f(x)是偶函数(答案为 A)
3、在△ABC中,∠C=90°,∠B=30°,D是BC上的一点,∠ADB=135°,AC=2,则BD等于()。
答 案:B
解 析:由已知得,AC=CD=2,设BD=x,在Rt△ABC中,BC=2cot30°=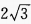
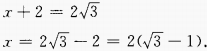
4、设集合M={0,1,2,3,4},N={1,2,3},T={2,4,6},则集合(M∩T)∪N=()。
- A:{0,1,2,3,4,6}
- B:{1,2,3,4}
- C:{2,4}
- D:{2,4,6}
答 案:B
解 析:M∩T=(2,4),则集合(M∩T)∪N={1,2,3,4}。答案为B。
主观题
1、化简: (1)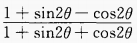
(2)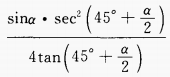
答 案:(1) (2)
(2)
2、设 (0<α<π),求tanα的值。
(0<α<π),求tanα的值。
答 案:
3、某气象预报站天气预报的准确率为80%,计算(1)5次预报中恰有4次准确的概率; (2)5次中至少有次准确的概率.(计算结果保留两个有效数字).
答 案: 把每次预报看做一次试验,“预报结果准确”看成事件P(A)=0.8,本题就相当于在5次独立重复试验中求A恰好发生4次(或至少4次)的概率,此题属于独立重复试验,由公式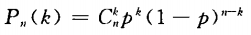 来求解。 (1)n=5;p=0.8;k=4
来求解。 (1)n=5;p=0.8;k=4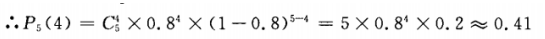 即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即
即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即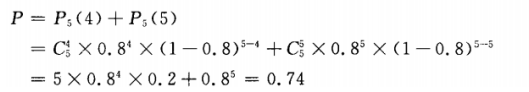 即至少有4次准确的概率为0.74。
即至少有4次准确的概率为0.74。
4、已知等差数列前n项和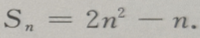 (Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
(Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
答 案: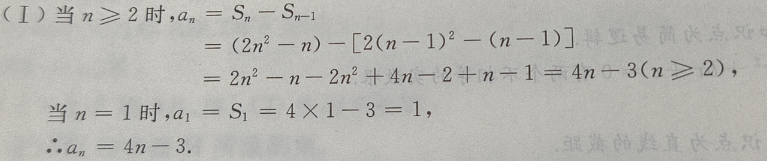

填空题
1、若A(3,a),B(-4,3)两点间的距离为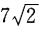 ,则a=______。
,则a=______。
答 案:a=-4或10
解 析:由两点间的距离公式得,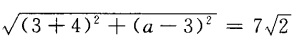 ,两边平方整理得(a-3)2=72→a-3=±7→a=-4或10。
,两边平方整理得(a-3)2=72→a-3=±7→a=-4或10。
2、y=ax2-bx+c的导数y'|x=1=______。
答 案:2a-b
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
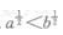
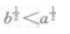
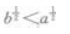 恒成立
恒成立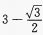
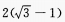
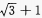
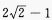
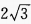
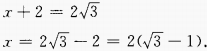
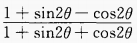
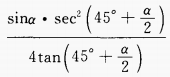
 (2)
(2)
 (0<α<π),求tanα的值。
(0<α<π),求tanα的值。
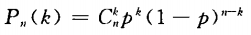 来求解。 (1)n=5;p=0.8;k=4
来求解。 (1)n=5;p=0.8;k=4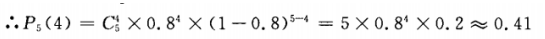 即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即
即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即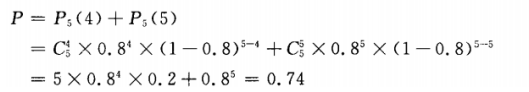 即至少有4次准确的概率为0.74。
即至少有4次准确的概率为0.74。
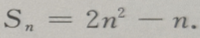 (Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
(Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和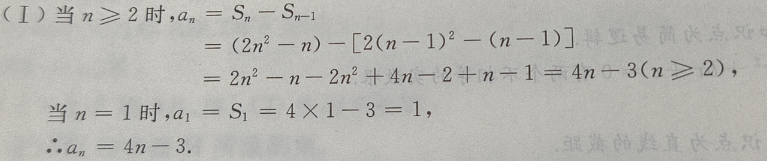

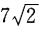 ,则a=______。
,则a=______。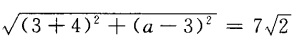 ,两边平方整理得(a-3)2=72→a-3=±7→a=-4或10。
,两边平方整理得(a-3)2=72→a-3=±7→a=-4或10。


