2024年成考高起点《数学(理)》每日一练试题10月28日

2024年成考高起点《数学(理)》每日一练试题10月28日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、设集合M={x||x-2|＜1}，N={x|x＞2}，则M∩N=（）

• A：{x|1＜x＜3}
• B：{x|x＞2}
• C：{x|2＜x＜3}
• D：{x|1＜x＜2}

答 案：C

解 析：M={x||x-2|＜1}解得{x|-1＜x-2＜1}={x|1＜x＜3}，故M∩N={x|2＜x＜3}

2、抛物线 y=ax²的准线方程是 y=2,则a=（）。

• A：
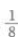
• B：
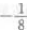
• C：8
• D：－8

答 案：B

解 析：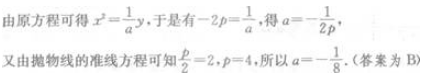

3、顶点在坐标原点，准线方程为y=4的抛物线方程式（）。

• A：
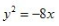
• B：
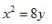
• C：
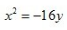
• D：

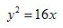
答 案：C

4、已知点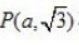在曲线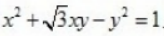上，那么a的值是（）。

• A：1
• B：1或-4
• C：-4或-1
• D：-4

答 案：B

主观题

1、在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.

答 案：由△ABC的面积为得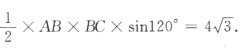所以AB =4.因此所以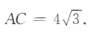

2、某工厂每月生产x台游戏机的收入为R(x)=+130x-206(百元)，成本函数为C(x)=50x+100(百元)，当每月生产多少台时,获利润最大?最大利润为多少?  

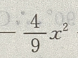答 案：利润 =收入-成本， L(x)=R(x)-C(x)=+130x-206-(50x+100)=+80x-306 法一：用二次函数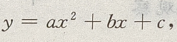当a<0时有最大值 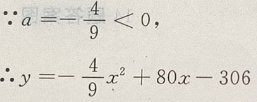是开口向下的抛物线，有最大值 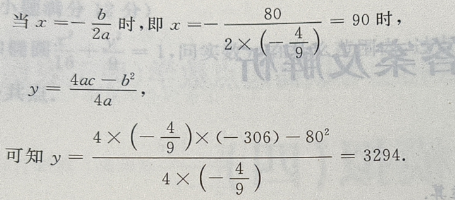法二：用导数来求解 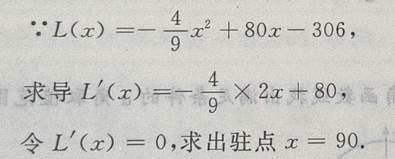因为x=90是函数在定义域内唯一驻点 所以x=90是函数的极大值点，也是函数的最大值点，其最大值为L（90）=3294  

3、求（1+tan10°）（1+tan35°）的值。  

答 案：原式=1+tan10°+tan35°+tan10°·tan35°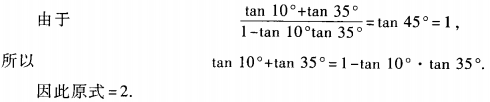

4、设函数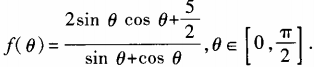（1）求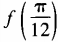；（2）求函数f（θ）最小值。

答 案：

填空题

1、长方体的长、宽、高分别为2,3,6，则该长方体的对角线长为（）

答 案：7

解 析：由题可知长方体的底面的对角线长为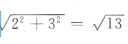，则在由高、底面对角线、长方体的对角线组成的三角形中，长方体的对角线长为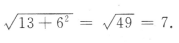

2、lg(tan43°tan45°tan47°)=（）  

答 案：0

解 析：lg(tan43°tan45°tan47°)=lg(tan43°tan45°cot43°)=lgtan45°=lg1=0