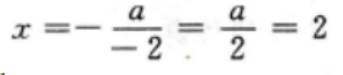课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(理)》每日一练试题10月17日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、若函数y=2x-1+3的反函数的图像经过点P,则点P的坐标是()。
- A:(1,2)
- B:(2,1)
- C:(2,5)
- D:(5,2)
答 案:D
解 析:反函数与原函数的x与y互换,原函数中,x=2时,y=5.故(5,2)为反函数图像上的点。答案为D。
2、使函数y=x2-2x-3为增函数的区间是()。
- A:(1,+∞)
- B:(-∞,3)
- C:(3,+∞)
- D:(-∞,1)
答 案:A
解 析:y’=2x-2,令y’=0得x=1,当x>1时,y’>0,原函数为增函数,所求区间为(1,+∞)
3、命题甲:实数a,b,c成等比数列;命题乙:b2=ac,则甲是乙()。
- A:充分条件但不是必要条件
- B:必要条件但不是充分条件
- C:充分必要条件
- D:不是充分条件也不是必要条件
答 案:A
4、已知a,b为任意正实数,则下列等式中恒成立的是()。
- A:ab=ba
- B:2a+b=2a+2b
- C:
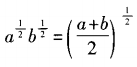
- D:algb=blga
答 案:D
解 析:由于a,b为任意正实数,不妨取a=1,b=2。在A项中,12≠21;B项中,21+2≠21+22;C项中,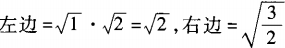 ,而
,而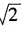 ≠
≠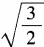 。故选D。
。故选D。
主观题
1、已知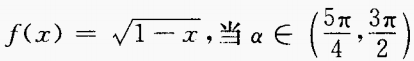 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。
答 案:由已知得,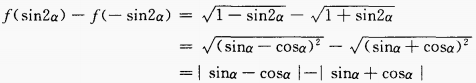
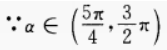 ∴sinα
∴sinα
2、试证明下列各题
(1)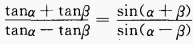
(2)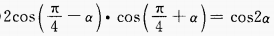
答 案:(1)化正切为正、余弦,通分即可得证。 (2)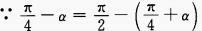

3、设 (0<α<π),求tanα的值。
(0<α<π),求tanα的值。
答 案:
4、如图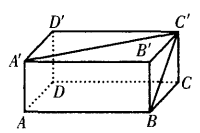 ,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
(2)A’B’和DD’的距离是多少?
答 案:(1)在长方体中BC和A’C’不在同一个平面内 所以BC和A’C’是异面直线 ∵在长方体中BC//B’C’ ∴∠A’C’B’是异面直线BC和A’C’所成的角
∵A’C’B’=45°
异面直线BC和A’C’所成的角是45°
(2)A’B’和DD’是异面直线
∵A’D’⊥A’B’ A’D’⊥DD’
∴A’D’的长即为异面直线A’B’和DD’的距离
∵A’D’=4
∴A’B’和DD’间的距离为4cm。
填空题
1、点B(4,-5)按向量a平移后的对应点B0(-4,7),则a的坐标是______。
答 案:(-8,12)
解 析:由平移公式得-4=4+a1,7=-5+a2→a1=-8,a2=12 ∴a的坐标是(-8,12)。
2、函数y=-x2+ax图像的对称轴为x=2,则a=______。
答 案:4
解 析:本题主要考查的知识点为二次函数的性质
由题意,该函数图像的对称轴为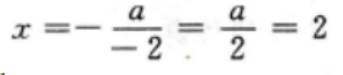
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
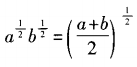
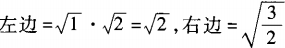 ,而
,而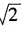 ≠
≠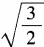 。故选D。
。故选D。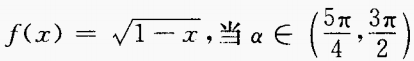 时,化简式子f(sin2α)-f(- sin2α)。
时,化简式子f(sin2α)-f(- sin2α)。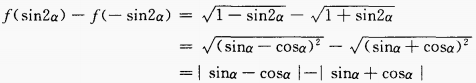
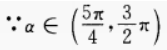 ∴sinα
∴sinα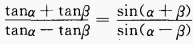
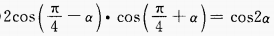
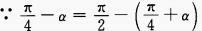

 (0<α<π),求tanα的值。
(0<α<π),求tanα的值。
 ,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?