课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(理)》每日一练试题10月12日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、下列各式的值为零的是()。
- A:00
- B:log11
- C:
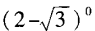
- D:log2|-1|
答 案:D
解 析:00和log11均没有意义,可排除(A)、(B),而(2-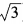 )0=1。故选D。
)0=1。故选D。
2、与1775°的终边相同的绝对值最小的角是()。
答 案:B
解 析:1775°=5×360°+(-25°),故所求角为-25°。
3、sinθ·cosθ·tanθ<0,则θ属于集合()。
- A:{θ|<0<π}
- B:{θ|<0<
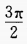 }
} - C:Ø
- D:{θ|-
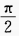 <θ<0}
<θ<0}
答 案:C
解 析:sinθ·cosθ·tanθ=sin2θ<0,这样的角不存在。
4、设函数f(x)=logax,且f(4)=2,则下列各式成立的是()。
- A:f(3)<O
- B:
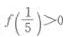
- C:f(5)<f(3)
- D:f(3)<f(5)
答 案:D
解 析:由f(4)-loga4=2,得a2=4,又a>0,故a=2,对于函数f(x)=logax,根据对数函数的性质有f(5)>f(3)成立.(答案为 D)
主观题
1、已知log53=a,log54=b,求log2512关于a,b的表达式。
答 案: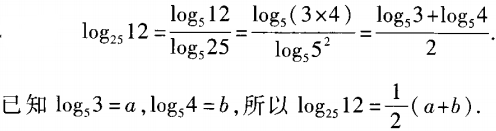
2、如图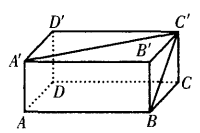 ,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
(2)A’B’和DD’的距离是多少?
答 案:(1)在长方体中BC和A’C’不在同一个平面内 所以BC和A’C’是异面直线 ∵在长方体中BC//B’C’ ∴∠A’C’B’是异面直线BC和A’C’所成的角
∵A’C’B’=45°
异面直线BC和A’C’所成的角是45°
(2)A’B’和DD’是异面直线
∵A’D’⊥A’B’ A’D’⊥DD’
∴A’D’的长即为异面直线A’B’和DD’的距离
∵A’D’=4
∴A’B’和DD’间的距离为4cm。
3、记△ABC的内角A,B,C的对边分别为a,b,c,已知B=60°,b2=ac,求A。
答 案:由余弦定理b2=a2+c2-2accosB,可得ac=a2+c2-ac,即a2+c2-2ac=(a-c)2=0,解得a=c。
又因为B=60°,故△ABC为等边三角形,所以A=60°
4、设 分别讨论x→0及x→1时f(x)的极限是否存在?
分别讨论x→0及x→1时f(x)的极限是否存在?
答 案: ∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
填空题
1、已知≤0<2π,且实数x满足log3x=2-cos2θ+sin2θ,则x的最小值是______。
答 案:3
解 析:因为log3x=2-(cos2θ-sin2θ)=2-cos2θ。 又log3x中的底数3>1,因此要使x最小,应使2-cos2θ的值最小,而其最小值为1,故x=3。
2、ABCD是正方形,E是AB的中点,如将△DAE和△CBE分别沿虚线DE、CE折起,使AE与BE重合如图 ,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
答 案:二面角为30°,PE与面ECS成60角°
解 析:(1)求面PCD与面ECD所成的二面角为多少度,就是要求出由平面PCD与平面ECD所组成的二面角的平面角,其中画出二面角的平面角是关键,因为二面角确定以后,二面角的平面角很容易画出(由二面角的平面角的定义)。求角度时,常用到勾股定理、正弦定理、余弦定理、兰垂线定理和逆定理。 (2)求PE与面ECD成多少度,就是求直线与平面所成的角是多少度。首先要找出平面的一条斜线(直线PE)和斜线的射影,斜线和射影所成的锐角,就是直线PE和平面ECD所成的角,再求出角度。 设CD的中点为F,练PF,EF
∵PC=PD,EC=ED.
∴PF⊥CD,EF⊥CD(三垂线定理)
∠PFE是二面角P-CD-E的平面角
∵PE⊥PC,PE⊥CD.
∴PE⊥平面PCD,又PF在平面PCD内
∴PE⊥PF
设正方形边长为1(如图)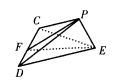
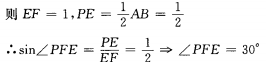 故面PCD与面ECD所成的二面角为30°,PE与面ECS成60角°。
故面PCD与面ECD所成的二面角为30°,PE与面ECS成60角°。
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
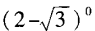
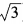 )0=1。故选D。
)0=1。故选D。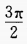 }
}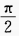 <θ<0}
<θ<0}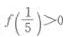
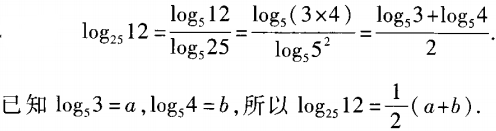
 ,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?  分别讨论x→0及x→1时f(x)的极限是否存在?
分别讨论x→0及x→1时f(x)的极限是否存在? ∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在
∴f(x)在x=0处极限不存在 同理f(x)在x=1处极限存在 ,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
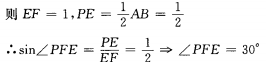 故面PCD与面ECD所成的二面角为30°,PE与面ECS成60角°。
故面PCD与面ECD所成的二面角为30°,PE与面ECS成60角°。


