2024年成考高起点《数学(理)》每日一练试题10月07日
2024-10-07 12:05:34 来源:吉格考试网
2024年成考高起点《数学(理)》每日一练试题10月07日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、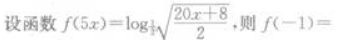 ()。
()。
- A:
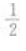
- B:
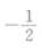
- C:2
- D:-2
答 案:B
解 析: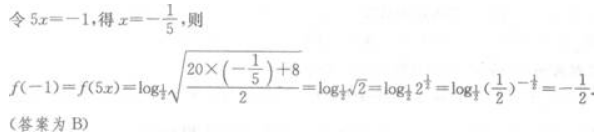
2、一个袋子中装有标号分别为1,2,3,4的四个球,采用有放回的方式从袋中摸球两次,每次摸出一个球,则恰有一次摸出2号球的概率为()。
- A:
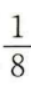
- B:

- C:
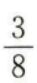
- D:

答 案:C
解 析:本题主要考查的知识点为独立重复试验的概率。 所求概率为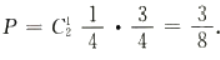
3、从1、2、3、4、5、6、7、8、9这九个数字中,随机取出一个数字,这个数字是奇数的概率是()。
- A:
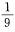
- B:
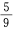
- C:
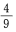
- D:
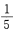
答 案:B
解 析:本题的试验是从1~9这九个数字中任取一个数字,显然选中其中任一个数字的可能 性都是相同的,属于等可能事件的概率,∵n=9,其中奇数个数m=5,∴其概率是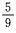 ,故选B。
,故选B。
4、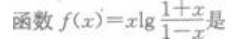 ()。
()。
- A:奇函数
- B:偶函数
- C:非奇非偶函数
- D:无法判断
答 案:B
解 析: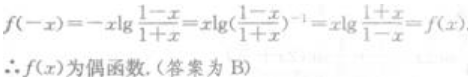
主观题
1、已知函数f(x)=(x-4)(x2-a) (I)求f"(x); (Ⅱ)若f"(-1)=8,求f(x)在区间[0,4]的最大值与最小值
答 案: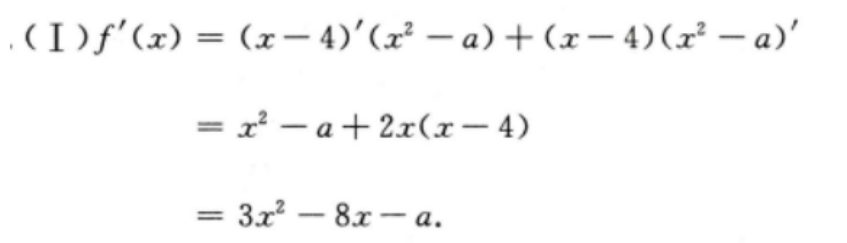

2、已知关于x的二次方程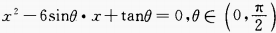 的两根相等,求sinθ+cosθ的值。
的两根相等,求sinθ+cosθ的值。
答 案:

3、某气象预报站天气预报的准确率为80%,计算(1)5次预报中恰有4次准确的概率; (2)5次中至少有次准确的概率.(计算结果保留两个有效数字).
答 案: 把每次预报看做一次试验,“预报结果准确”看成事件P(A)=0.8,本题就相当于在5次独立重复试验中求A恰好发生4次(或至少4次)的概率,此题属于独立重复试验,由公式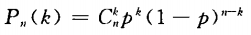 来求解。 (1)n=5;p=0.8;k=4
来求解。 (1)n=5;p=0.8;k=4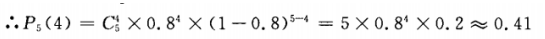 即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即
即恰有4次准确的概率为0.41.
(2)5次至少有4次准确的概率,就是5次中恰有4次准确的概率与5次预报中都准确的概率的和,即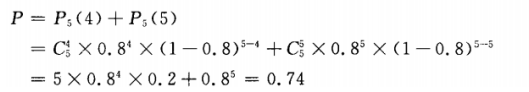 即至少有4次准确的概率为0.74。
即至少有4次准确的概率为0.74。
4、记△ABC的内角A,B,C的对边分别为a,b,c,已知B=60°,b2=ac,求A。
答 案:由余弦定理b2=a2+c2-2accosB,可得ac=a2+c2-ac,即a2+c2-2ac=(a-c)2=0,解得a=c。 又因为B=60°,故△ABC为等边三角形,所以A=60°
填空题
1、一个问题在1小时内,甲能独立解决的概率是0.5,乙能独立解决的概率是0.4,两人在1小时内解决问题的概率是______。
答 案:0.7
解 析:设事件A为两人在1小时内解决问题,即1小时内至少有一人能解决问题,事件B为甲在1小时内解决问题,事件C为乙在1小时内解决问题,事件B、C是相互独立事件,事件A的对立事件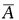 互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(
互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(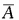 )=1-P(
)=1-P(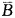 ·
·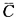 )=1-P(
)=1-P(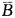 )·P(
)·P(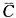 )
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
)
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
2、函数 的定义域是()
的定义域是()
答 案: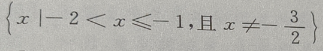
解 析: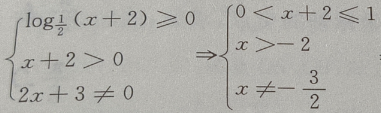
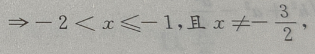 所以函数
所以函数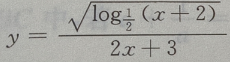 的定义域是
的定义域是