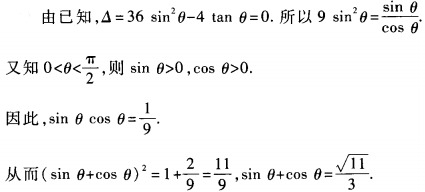2024年成考高起点《数学(理)》每日一练试题10月06日

2024年成考高起点《数学(理)》每日一练试题10月06日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、一部电影在4个单位轮映，每一单位放映一场，轮映次序有（）。

• A：4种
• B：16种
• C：24种
• D：256种

答 案：C

2、以抛物线y²＝8x的焦点为圆心，且与此抛物线的准线相切的圆的方程是（）。

• A：（x＋2）²＋y²＝16
• B：（x＋2）²＋y²＝4
• C：（x－2）²＋y²＝16
• D：（x－2）²＋y²＝4

答 案：C

解 析：抛物线y²＝8x的焦点，即圆心为（2，0），抛物线的准线方程是x＝-2，与此抛物线的准线相切的圆的半径是r＝4，与此抛物线的准线相切的圆的方程是（x－2）²＋y²＝16。答案为C。

3、过直线3x＋2y＋1＝0与2x－3y＋5＝0的交点，且垂直于直线L：6x－2y＋5＝0的直线方程是（）。

• A：x－3y－2＝0
• B：x＋3y－2＝0
• C：x－3y＋2＝0
• D：x＋3y＋2＝0

答 案：B

解 析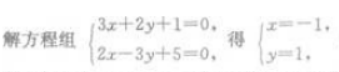： 即两直线的交点坐标为（-1,1） 又直线L:6x-2y+5=0的斜率为3 ，则所求的直线方程为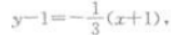即x+3y-2=0.

4、过A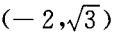B（-5，0）两点直线的倾斜角为（）。

• A：
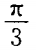
• B：
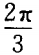
• C：
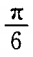
• D：

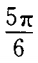
答 案：C

解 析：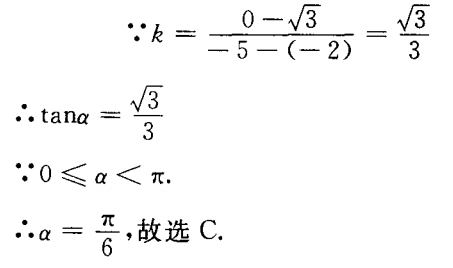

主观题

1、在△ABC中如果sinA=2sinBcosC，求证：△ABC是等腰三角形。  

答 案：∴△ABC为等腰三角形。

2、记△ABC的内角A，B，C的对边分别为a，b，c，已知B=60°，b²=ac，求A。    

答 案：由余弦定理b²=a²+c²-2accosB，可得ac=a²+c²-ac，即a²+c²-2ac=(a-c)²=0，解得a=c。 又因为B=60°，故△ABC为等边三角形，所以A=60°

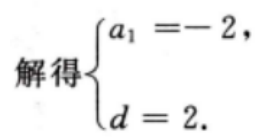
3、已知等差数列｛an｝中，a1+a2+a3=6,a2+a4+a5= 12求｛an｝的首项与公差。  

答 案：因为｛an｝为等差数列，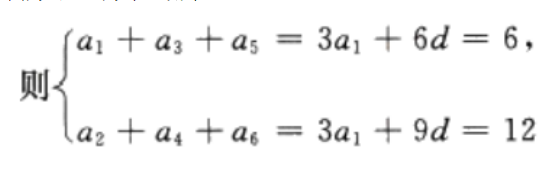

4、已知a^m=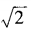，an=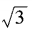，求a3^n-4m的值。  

答 案：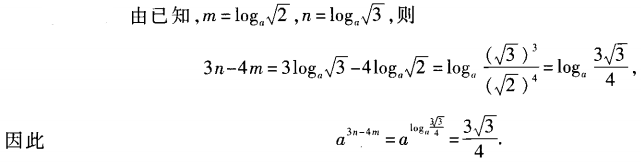

填空题

1、若P（3，2）是连接P1（2，y）和P2（x，6）线段的中点，则x=______，y=______。  

答 案：x=4，y=-2  

解 析：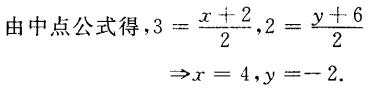

2、已知关于t的二次方程t2-6tsinθ+tanθ=0（0＜θ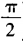＜）的两根相等，则sinθ+cosθ的值等于______。

答 案：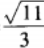

解 析：