2024年成考高起点《数学(文史)》每日一练试题09月29日

2024年成考高起点《数学(文史)》每日一练试题09月29日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、在∆ABC中，∠ABC=600，AB=4，BC=6，则AC=（）。

• A：128
• B：76
• C：
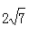
• D：

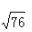
答 案：C

2、设M=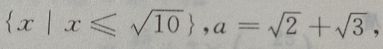那么（）

• A：
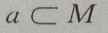
• B：
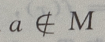
• C：
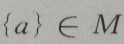
• D：

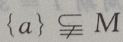
答 案：D

解 析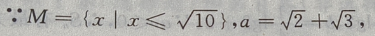： M是集合，a为元素，{a}为集合，元素与集合的关系是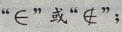集合与集合的关系是  

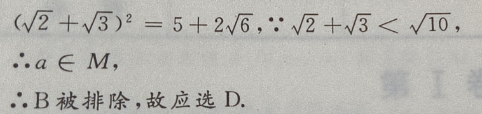
3、A、B是抛物线y²=8x上两点，且此抛物线的焦点在线段AB上，已知A、B两点的横坐标之和为10，则|AB|=（）。

• A：18
• B：14
• C：12
• D：10

答 案：B

解 析：因为焦点F在AB上,则有FA=A到准线的距离=X1+P/2FB=B到准线的距离=X2+P/2所以,AB=FA+FB=X1+X2+P
又有X1+X2=10.P=4
故有：AB=10+4=14

4、函数y=-x²+2x的值域是（）。  

• A：[0,+∞)
• B：[1,+∞)
• C：(-∞,1]
• D：(-∞,0)

答 案：C

解 析：本题主要考查的知识点为函数的值域. y=-x²+2x=1-(x-1)²≤1，故原函数的值域为(-∞,1]

主观题

1、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

2、在△ABC中，已知AB=2,BC=1,CA=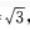 点D,E,F分别在AB,BC,CA边上，△DEF为正三角形，记∠FEC为α，如果sinα= 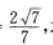求△DEF的边长。

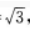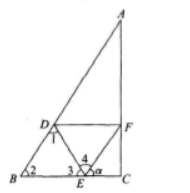
答 案：解析:由AB=2，BC=1,CA= 得BC²=CA²=AB²,因此∠C=90°，如图所示。 因为sinA= 所以∠A=30°，于是∠b=60°。 设正△DEF边长为l，已知AB=2,sinα=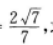 由此EC=lcosα 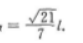有图知，∠1+∠2+∠3=180°（三角形内角和）； ∠3+∠4+α=180°，因为∠2-∠4=60°，所以∠1=α。 【考点指要】本题主要考查三角函数的概念、同角三角函数的关系及正弦定理，这些均是考试大纲要求掌握的重要概念，并要求能达到灵活应用的程度，此类题是在成人高考中出现频率较高的题型，

3、已知三角形的三边边长组成公差为1的等差数列，且最大角是最小角的二倍，求三边之长。  

答 案：三角形的三边边长分别为4，5，6。

4、设函数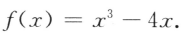
(I）求f'(2)；
(II）求f(x）在区间[一1,2]的最大值与最小值．

答 案：(I）因为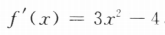，所以f'(2)=3×2²-4=8.(II）因为x＜-1，f(-1)=3.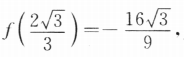f(2)=0.
所以f(x）在区间[一1,2]的最大值为3，最小值为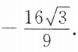

填空题

1、函数f(x)=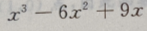在区间[-3,3]上的最大值为（）  

答 案：4

解 析：这题考的是高次函数的最值问题，可用导数来求函数在区间[-3,3]上的最值。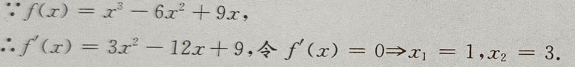 列出表格 由上表可知函数在[-3,3]上，在x=1点处有最大值为4.  

2、在∆ABC中，已知cosA=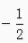，cosB=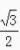，那么cosC=______。

答 案：