2022年成考高起点《数学(文史)》每日一练试题11月12日

2022年成考高起点《数学(文史)》每日一练试题11月12日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共有 ( )

• A：7种
• B：4种
• C：5种
• D：6种

答 案：C

2、设集合M={a，b｝，N={b，c｝，满足的集合，P的个数是（）。

• A：6
• B：7
• C：8
• D：9

答 案：B

解 析：由已知条件得：M∪N=｛a，b，c｝，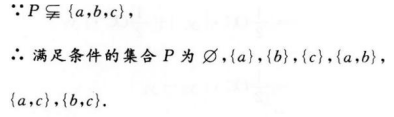

3、设sinx=1/2，则sin2xcos³x=（）。

• A：9/16
• B：7/16
• C：1/4
• D：3/4

答 案：A

解 析：sin2x=2sinxcosx，sin2xcos³x=2sinxcos⁴x，sinx=1/2，所以cos²x=1-1/4=3/4，cos⁴x=9/16，所以原式=2x1/2x9/16=9/16。

4、甲、乙、丙、丁4人排成一行，其中甲、乙必须排在两端，则不同的排法共有（）

• A：4种
• B：2种
• C：8种
• D：24种

答 案：A

解 析：甲乙必须排在两端的排法有C₂¹·A₂²=4种.

主观题

1、

答 案：

2、已知等差数列{a_n}中，a₃+a₄+a₅=6。
（Ⅰ）求a₄的值；
（Ⅱ）若a₁=-4，求{a_n}的通项公式。

答 案：（Ⅰ）由等差数列的基本性质，a₃+a₄+a₅=3a₄=6，a₄=2。
（Ⅱ），a₄-a₁=3d=2+4=6所以d=2，所以数列{a_n}的通项公式即a_n=-4+(n-1)d=-4+(n-1)x2=2n-6。

3、在△ABC中，已知三边a、b、c成等差数列，且最大角∠A是最小角的2倍，求a：b：c。

答 案：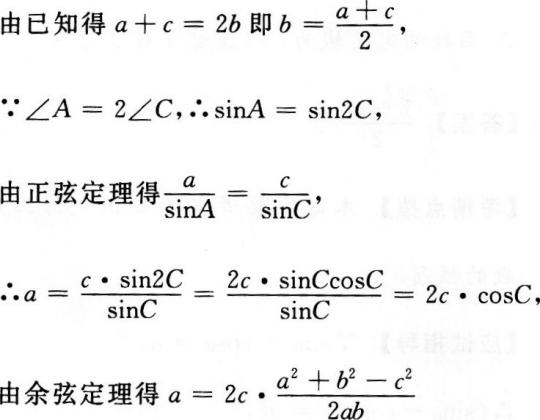

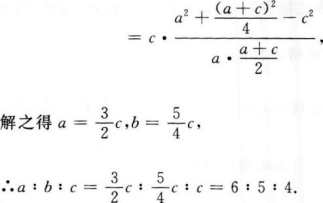
4、已知函数f(x)=x³+x²-5x-1。求：(1)f(x)的单调区间; (2)f(x)零点的个数。

答 案：

填空题

1、若平面向量a=(x,1)，b=(1,-2),且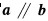，则x=

答 案：-1/2

2、已知曲线y=lnx+a在点(1，a)处的切线过点(2，-1)，则a=______。

答 案：-2

解 析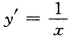：，故曲线在点(1，a)处的切线的斜率为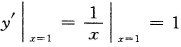，因此切线方程为：y-a=x-1，即y=x-1+a，又切线过点(2，-1)，因此有-1=2-1+a，故a=-2.