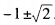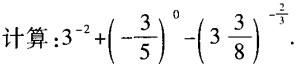2024年成考高起点《数学(文史)》每日一练试题09月25日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、用1,2,3,4一组成没有重复数字的三位数,其中偶数共有()
答 案:B
解 析:若三位数为偶数,个位数只能从2,4中选一个,故没有重复数字的偶数三位数为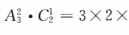
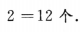
2、若角α终边上有一点P(3a,-4a),a<0,则sinα·tanα的值是()。
答 案:C
3、设集合M={a,b,c,d},N=(a,b,c),则集合M∪N=()。
- A:{a,b,c}
- B:{d}
- C:{a,b,C,d}
- D:空集
答 案:C
4、某单位有4名男同志和3名女同志,现要组成一个有男有女的小组,规定小组中男同志的数目为偶数,女同志的数目为奇数,则共有组织方法种数是( )
答 案:B
解 析:首先确定这是一个组合问题,因为组成小组的人员与排列顺序无关.其次按照题意可知:虽然组成小组的人数可以不限,但必须同时有男同志和女同志,而且男同志人数必须为偶数,女同志人数必须为奇数.由此可知:当男同志为2人时,女同志可为1人或3人,当男同志为4人 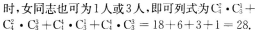 【考点指要】本题考点在于会正确判断给定问题是排列问题还是组合问题,并且会解排列、组合的简单应用题.排列、组合的简单应用题是近几年成人高考的必考内容.
【考点指要】本题考点在于会正确判断给定问题是排列问题还是组合问题,并且会解排列、组合的简单应用题.排列、组合的简单应用题是近几年成人高考的必考内容.
主观题
1、求证:双曲线的一个焦点到一条渐近线的距离等于虚半轴的长.
答 案:设双曲线的方程为 则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为
则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为 令设焦点F2(c,0)到渐近线
令设焦点F2(c,0)到渐近线 的距离为d,则
的距离为d,则 即从双曲线
即从双曲线 的一个焦点F2(c,0)到一条渐近线
的一个焦点F2(c,0)到一条渐近线 的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线
的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线 以及点F1(-c,0)到渐近线
以及点F1(-c,0)到渐近线 的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
解 析:本题考查的是圆锥曲线与直线位置关系的推理能力,主要是用代数的方法表示几何中的问题.考生必须对曲线方程、几何性质及元素之间的关系有深刻的理解,方可解决此类综合题.这种综合性的圆锥曲线试题出现的概率比较高,要引起重视.
2、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35° 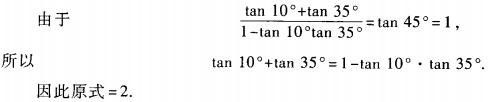
3、(1)已知tanα=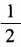 求cot2α的值; (2)已知tan2α=1,求tanα的值。
求cot2α的值; (2)已知tan2α=1,求tanα的值。
答 案:(1)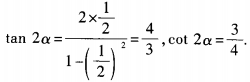 (2)由已知,得
(2)由已知,得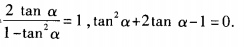 解关于tanα的一元二次方程,得tanα=
解关于tanα的一元二次方程,得tanα=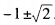
4、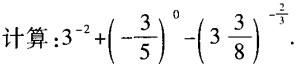
答 案:
填空题
1、设直线y=2x+m与抛物线y2=4x没有公共点,则m的取值范围是______。
答 案:
2、点(4,5)关于直线y=x的对称点的坐标为()
答 案:(5,4)
解 析:点(4,5)关于直线y=x的对称点为(5,4).
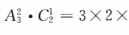
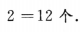
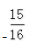
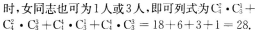 【考点指要】本题考点在于会正确判断给定问题是排列问题还是组合问题,并且会解排列、组合的简单应用题.排列、组合的简单应用题是近几年成人
【考点指要】本题考点在于会正确判断给定问题是排列问题还是组合问题,并且会解排列、组合的简单应用题.排列、组合的简单应用题是近几年成人 则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为
则它的焦点坐标为F1(-c,0),F2(c,0),其中c2=a2+b2,渐近线方程为 令设焦点F2(c,0)到渐近线
令设焦点F2(c,0)到渐近线 的距离为d,则
的距离为d,则 即从双曲线
即从双曲线 的一个焦点F2(c,0)到一条渐近线
的一个焦点F2(c,0)到一条渐近线 的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线
的距离等于虚半
轴的长b,由上述推导过程可知,点F2到渐近线 以及点F1(-c,0)到渐近线
以及点F1(-c,0)到渐近线 的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.
的距离都等。
由于证明中只涉及a,b,c,而与双曲线的位置无关,所以这个结论对于任意双曲线都成立.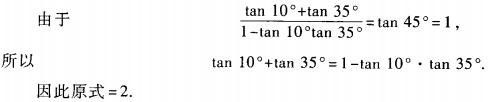
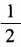 求cot2α的值; (2)已知tan2α=1,求tanα的值。
求cot2α的值; (2)已知tan2α=1,求tanα的值。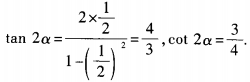 (2)由已知,得
(2)由已知,得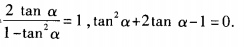 解关于tanα的一元二次方程,得tanα=
解关于tanα的一元二次方程,得tanα=