课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(理)》每日一练试题09月23日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、已知sinα=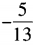 ,且540°<α<630°,则sin2α=()。
,且540°<α<630°,则sin2α=()。
答 案:B
解 析:由已知,360°+180°<α<360°+270°,所以α是第三象限的角,故 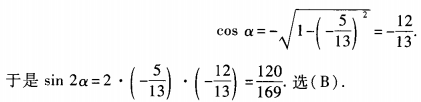
2、下列各等式不成立的是()。
- A:3x·2x=6x
- B:9x=(3x)2
- C:
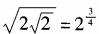
- D:
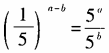
答 案:D
解 析:3x·2x=(3·2)x=6x,排除A;(3x)2=(32)x=9x,排除B;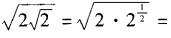
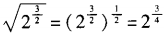 ,排除C。选D。
,排除C。选D。
3、若f(x)为偶函数,且在(0,+∞)为增函数,则下列不等式成立的是()。
答 案:B
解 析: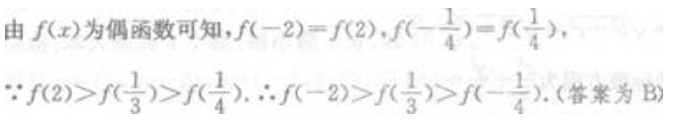
4、某类灯泡使用时数在1000小时以上的概率为0.2,三个灯泡在使用1000小时以后最多只有一个坏的概率为()
答 案:B
解 析:已知灯泡使用1000小时后好的概率为0.2,坏的概率为1-0.2=0.8,则三个灯泡使用1000小时以后,可分别求得: P(没有坏的)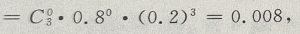 P(一个坏的)
P(一个坏的)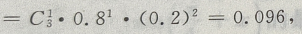 故最多只有一个坏的概率为:0.008+0.096=0.104.
故最多只有一个坏的概率为:0.008+0.096=0.104.
主观题
1、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得 AB=120m,求河的宽
AB=120m,求河的宽

答 案:如图,  ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m
2、化简: (1)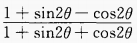
(2)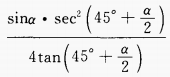
答 案:(1) (2)
(2)
3、已知数列{an}中,a1=2,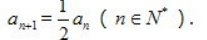 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
答 案:解:
4、已知一组数据9.9;10.3;9.8;10.1;10.4;10;9.8;9.7,计算这组数据的方差。
答 案:
填空题
1、若tanα-cotα=1,则 =______。
=______。
答 案:4
解 析:由立方差公式得,tan3α-cot3α=(tana-cotα)(tan2α+tanαcota+cot2α)(tana-cotα)[(tanα-cotα)2+3tanαcotα]=4
2、一个问题在1小时内,甲能独立解决的概率是0.5,乙能独立解决的概率是0.4,两人在1小时内解决问题的概率是______。
答 案:0.7
解 析:设事件A为两人在1小时内解决问题,即1小时内至少有一人能解决问题,事件B为甲在1小时内解决问题,事件C为乙在1小时内解决问题,事件B、C是相互独立事件,事件A的对立事件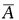 互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(
互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(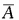 )=1-P(
)=1-P(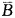 ·
·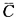 )=1-P(
)=1-P(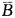 )·P(
)·P(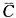 )
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
)
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
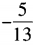 ,且540°<α<630°,则sin2α=()。
,且540°<α<630°,则sin2α=()。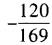
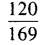
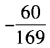
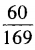
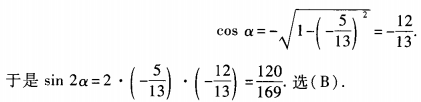
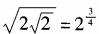
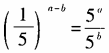
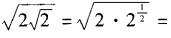
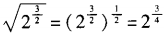 ,排除C。选D。
,排除C。选D。
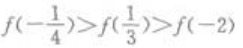
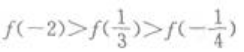
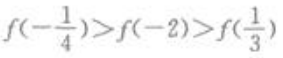
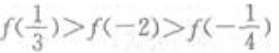
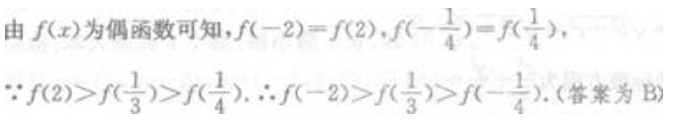
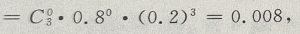 P(一个坏的)
P(一个坏的)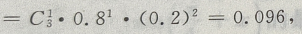 故最多只有一个坏的概率为:0.008+0.096=0.104.
故最多只有一个坏的概率为:0.008+0.096=0.104.
 AB=120m,求河的宽
AB=120m,求河的宽

 ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m
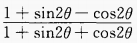
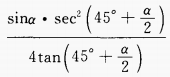
 (2)
(2)
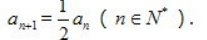 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5

 =______。
=______。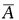 互为在1小时内两个人都没有解决问题,所以 P(A)=1-P(
互为在1小时内两个人都没有解决问题,所以 P(A)=1-P( )=1-P(
)=1-P(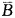 ·
·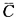 )=1-P(
)=1-P(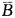 )·P(
)·P(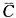 )
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7
)
=1-(1-0.5)×(1-0.4)=1-(0.5×0.6)=1-0.3=0.7


