2024年成考高起点《数学(理)》每日一练试题09月10日

2024年成考高起点《数学(理)》每日一练试题09月10日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、若f(x)为偶函数，且在(0，＋∞)为增函数，则下列不等式成立的是（）。

• A：
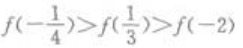
• B：
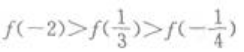
• C：
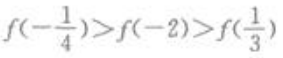
• D：

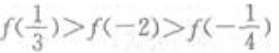
答 案：B

解 析：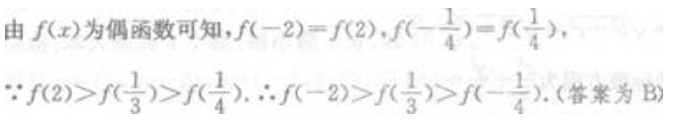

2、下列各等式不成立的是（）。

• A：3^x·2^x=6^x
• B：9^x=（3^x）2
• C：
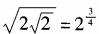
• D：

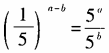
答 案：D

解 析：3^x·2^x=（3·2）^x=6^x，排除A；（3^x）²=（3²）^x=9^x，排除B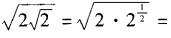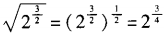；，排除C。选D。  

3、以椭圆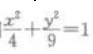上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于（）。

• A：
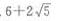
• B：
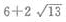
• C：
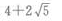
• D：

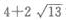
答 案：A

解 析：由椭圆方程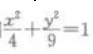 可知a²=9,b²=4,则 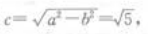则椭圆上任一点(长轴两端除外)和两个焦点为顶点的三角形的周长等于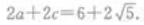

4、直线2x+y+m=0和直线x+2y+n=0的位置关系是（）。

• A：平行
• B：垂直
• C：相交但不垂直
• D：不确定

答 案：C

解 析：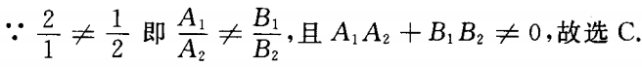

主观题

1、计算。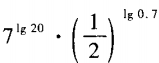  

答 案：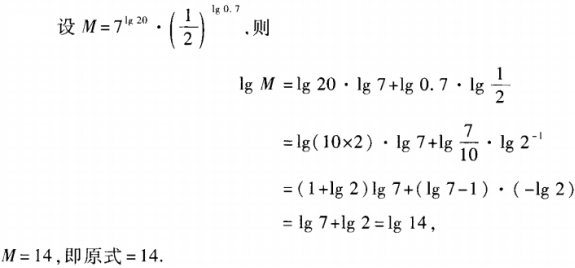

2、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得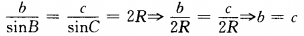

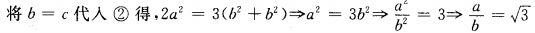
∴a：b=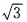：1
于是a：b：c=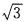：1：1。  

3、某工厂每月生产x台游戏机的收入为R(x)=+130x-206(百元)，成本函数为C(x)=50x+100(百元)，当每月生产多少台时,获利润最大?最大利润为多少?  

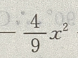答 案：利润 =收入-成本， L(x)=R(x)-C(x)=+130x-206-(50x+100)=+80x-306 法一：用二次函数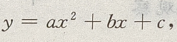当a<0时有最大值 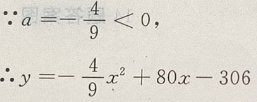是开口向下的抛物线，有最大值 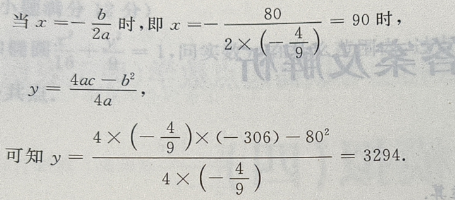法二：用导数来求解 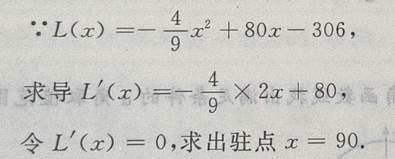因为x=90是函数在定义域内唯一驻点 所以x=90是函数的极大值点，也是函数的最大值点，其最大值为L（90）=3294  

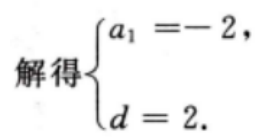
4、已知等差数列｛an｝中，a1+a2+a3=6,a2+a4+a5= 12求｛an｝的首项与公差。  

答 案：因为｛an｝为等差数列，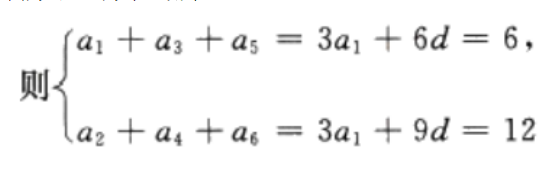

填空题

1、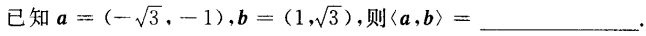  

答 案：；150°

解 析：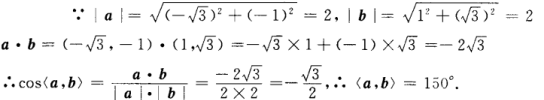

2、已知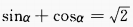，则=______。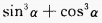  

答 案：

解 析：