课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(文史)》每日一练试题08月16日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、不等式|3x+1|≤2的解集是( )
答 案:A
解 析:不等式|3x+1|≤2的解集是不等式3x+1≤2与3x+1≥-2的解集的交集,因此原不等式可写成-2≤3x+1≤2,即-3≤3x≤1,-1≤x≤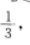 在用集合表示x的解集为
在用集合表示x的解集为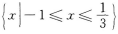 【考点指要】本题主要考查绝对值不等式的解法以及会用集合表示不等式的解集,此类题是成人高考常出现的题型.
【考点指要】本题主要考查绝对值不等式的解法以及会用集合表示不等式的解集,此类题是成人高考常出现的题型.
2、下列各选项中,正确的是()。
- A:y=x+sinx是偶函数
- B:y=x+sinx是奇函数
- C:y=|x|+sinx是偶函数
- D:y=|x|+sinx是奇函数
答 案:B
3、点(2,4)关于直线y=x的对称点的坐标为()
- A:(4,2)
- B:(-2,-4)
- C:(-2,4)
- D:(-4,-2)
答 案:A
解 析:点(2,4) 关于直线y=x对称的点为(4,2)
4、已知函数f(x)=cos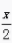 ,则下列等式中对于任意x都成立的是()。
,则下列等式中对于任意x都成立的是()。
- A:f(x+2π)=f(x)
- B:f(π-x)=f(x)
- C:f(-x)=f(x)
- D:f(-x)=-f(x)
答 案:C
主观题
1、已知a-a-1=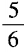 ,求a3-a-3的值。
,求a3-a-3的值。
答 案:
2、求下列函数的最大值、最小值和最小正周期: (1)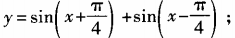 2)y=6cosx+8sinx
2)y=6cosx+8sinx
答 案: 所以函数的最大值是
所以函数的最大值是 最小值是
最小值是 最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为
最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π
因此,函数的最大值是10,最小值是-10,最小正周期为2π
3、设椭圆的中心是坐标原点,长袖在x轴上,离心率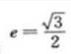 ,已知点P(0,3/2)到椭圆上的点的最远距离是
,已知点P(0,3/2)到椭圆上的点的最远距离是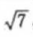 ,求椭圆的方程。
,求椭圆的方程。
答 案:
4、已知am=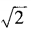 ,an=
,an=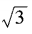 ,求a3n-4m的值。
,求a3n-4m的值。
答 案: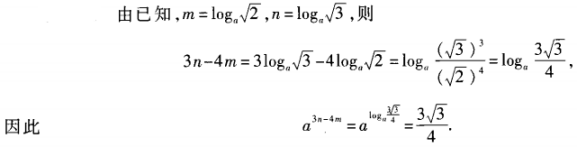
填空题
1、曲线在点(1,1)处的切线方程是______。
答 案:2x+y-3=0
解 析:本题主要考查的知识点为切线方程。
由题意,该切线斜率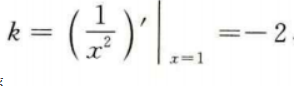 ,又过点(1,1),所以切线方程为y-1=-2(x-1),即2x+y-3=0。
,又过点(1,1),所以切线方程为y-1=-2(x-1),即2x+y-3=0。
2、log2[log2(log381)]=______。
答 案:1
解 析:由于log381=log334=4,于是 原式=log2(log24)=log22=1。
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
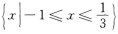
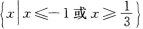
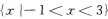
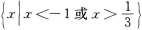
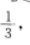 在用集合表示x的解集为
在用集合表示x的解集为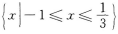 【考点指要】本题主要考查绝对值不等式的解法以及会用集合表示不等式的解集,此类题是成人
【考点指要】本题主要考查绝对值不等式的解法以及会用集合表示不等式的解集,此类题是成人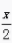 ,则下列等式中对于任意x都成立的是()。
,则下列等式中对于任意x都成立的是()。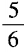 ,求a3-a-3的值。
,求a3-a-3的值。

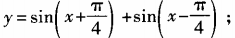 2)y=6cosx+8sinx
2)y=6cosx+8sinx 所以函数的最大值是
所以函数的最大值是 最小值是
最小值是 最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为
最小正周期为2π,
(2)要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式,需使cosx与sinx的系数平方和为1,为此,将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π
因此,函数的最大值是10,最小值是-10,最小正周期为2π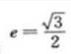 ,已知点P(0,3/2)到椭圆上的点的最远距离是
,已知点P(0,3/2)到椭圆上的点的最远距离是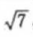 ,求椭圆的方程。
,求椭圆的方程。
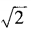 ,an=
,an=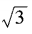 ,求a3n-4m的值。
,求a3n-4m的值。
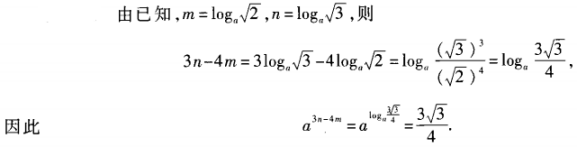
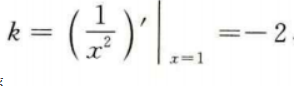 ,又过点(1,1),所以切线方程为y-1=-2(x-1),即2x+y-3=0。
,又过点(1,1),所以切线方程为y-1=-2(x-1),即2x+y-3=0。


