2024年成考高起点《数学(理)》每日一练试题08月12日

2024年成考高起点《数学(理)》每日一练试题08月12日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、函数y=sin（x+11）的最大值是（）。

• A：11
• B：1
• C：-1
• D：-11

答 案：B

解 析：本题主要考查的知识点为三角函数的值域。 因为-1≤sin（wx+q）≤1，所以-1≤sin（x+11）≤1，故y=sin（x+11）的最大值为1。

2、在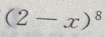的展开式中,的系数是

• A：448
• B：1140
• C：-1140
• D：-448

答 案：D

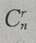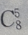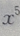解 析：直接套用二项式展开公式: 注:展开式中第r+1项的二项式系数与第r+1项的系数不同,此题不能只写出就为的系数  

3、在△ABC中,已知2B= A+C,= ac,则B-A=（）  

• A：0
• B：
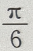
• C：
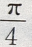
• D：

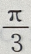
答 案：A

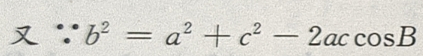
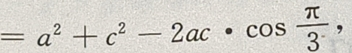
解 析：在△ABC中,A+B+C=π，A+C=π-B，① 因为2B=A+C，② 由①②得2B=π-B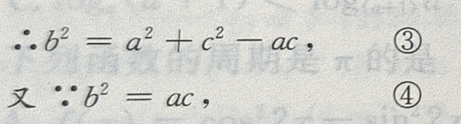， 由③④得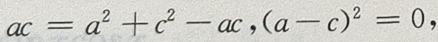a=c。所以A=C，又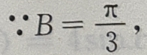所以△ABC为等边三角形，则B-A=0  

4、方程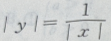的图像是下图中的（）  

• A：
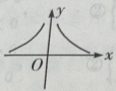
• B：
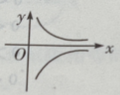
• C：
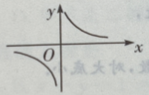
• D：

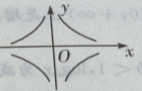
答 案：D

解 析：本题属于读图题型，在寻求答案时,要着重讨论方程的表达式  

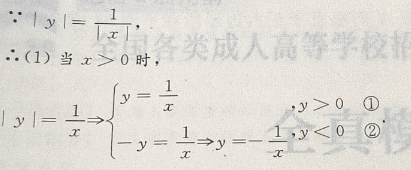
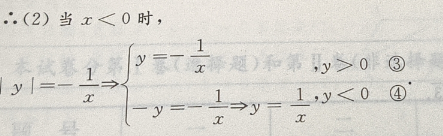
主观题

1、设函数f(x)= (Ⅰ)求f(x)的单调区间; (Ⅱ)求 f(x)的极值

答 案：(Ⅰ)函数的定义域为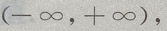 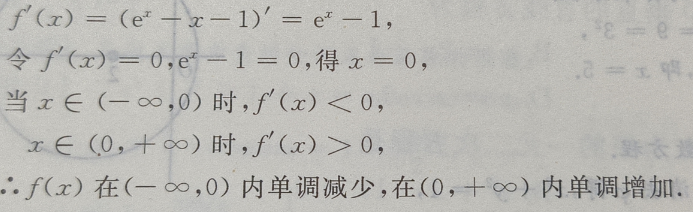(Ⅱ)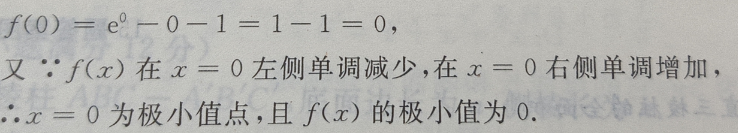  

2、已知数列的前n项和 求证：是等差数列，并求公差和首项。  

答 案：  

3、已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c．

答 案：由已知得解得

4、记△ABC的内角A，B，C的对边分别为a，b，c，已知B=60°，b²=ac，求A。    

答 案：由余弦定理b²=a²+c²-2accosB，可得ac=a²+c²-ac，即a²+c²-2ac=(a-c)²=0，解得a=c。 又因为B=60°，故△ABC为等边三角形，所以A=60°

填空题

1、曲线y=在点(1，1)处的切线方程是______。

答 案：2x+y-3=0

解 析：本题主要考查的知识点为切线方程 由题意，该切线斜率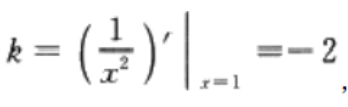， 又过点(1，1)，所以切线方程为y-1=-2(x-1)

2、函数的定义域是（）

答 案：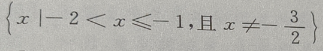

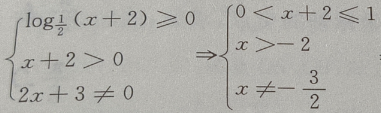
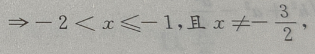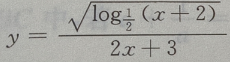解 析：所以函数的定义域是