2022年成考高起点《数学(文史)》每日一练试题10月23日

2022年成考高起点《数学(文史)》每日一练试题10月23日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共有 ( )

• A：7种
• B：4种
• C：5种
• D：6种

答 案：C

2、集合A=｛x|0≤x≤2｝，B=｛x|x≥1｝则集合A∩B=（）。

• A：｛x|x≥0｝
• B：｛x|x≥1｝
• C：｛x|0≤x≤1｝
• D：｛x|1≤x≤2｝

答 案：D

解 析：由集合的交集运算可知，A∩B=｛x|1≤x≤2｝。

3、抛物线 x²=−16y上一点P到焦点的距离是6，则点P的坐标是（）。

• A：(4√2,-2)
• B：(4√2,2)
• C：(4,-1)
• D：(-4,-1)

答 案：A

解 析：由x2=-16y可得 p=8，p2=4,∴F(0,-4)，∴准线方程y=4。由题意得lPF|=6，∴lPA|=6。∵|AB|=4，∴|PB|=2，∴P点的坐标为(x，-2)。∵P(x，-2)点在抛物线上，∴x2=−16×(−2)=32。所以是(-4√2,-2)或(4√2,-2)

4、从红黄绿三种颜料中，任选两种，以重量为1：1配成一种新颜色，能配成不同的种数为（）。

• A：6
• B：12
• C：3
• D：8

答 案：C

解 析：由已知条件可知颜色的配制与顺序无关属于组合问题，所以新颜色的种数为

主观题

1、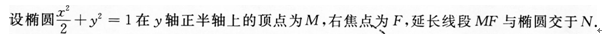 （I）求直线MF的方程；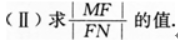

答 案：

2、已知△ABC中，A=60°，AB=AC=2，求:
（1）BC；
（2）△ABC的面积。

答 案：（1）A=60°且AB=AC=2，可知△ABC为等边三角形，所以BC=2。
（2）

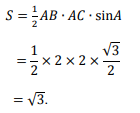
3、(Ⅱ)f(x)的单调区间，并指出f(x)在各个单调区间的单调性 　　 

答 案：由(I)知f(x)=x^3??-3/2x^2??-1/2 f(x)’=3x²-3x 令f(x)’=0,得x1=0，x2=1. 当x变化时，f(x)’，f(x)的变化情况如下表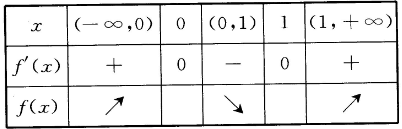： 即f(x)的单调区间为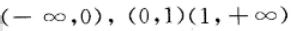,并且f(x)在上为增函数，在(0，1)上为减函数.         ???^?

4、已知三角形的一个内角是π/3，面积是10√3，周长是20，求各边的长。

答 案：设三角形三边分别为a，b，c，∠A=60°，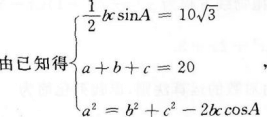
解之得a1=7,b1=5，c1=8或a2=7，b2=8，c2=5，故三边长分别为7，5，8。

填空题

1、拋物线y²= 2px的准线过双曲线x²/3-y²=1的左焦点，则p=

答 案：由题意知，p>抛物线y^2??= 2px的准线为x=-p/2，双曲线x^2??/3-y^2??=1的左焦点为 ，即(-2,0)，由题意知，-p/2 =-2,p =4

2、若向量a=（1，2）与b=（3，x）平行，则x= __________

答 案：1

解 析：【考情点拨】．本题主要考查的知识点为函数的极值．【应试指导】