2022年成考高起点《数学(理)》每日一练试题10月22日

2022年成考高起点《数学(理)》每日一练试题10月22日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、4x²-y²+1=0的渐近线方程为（）。

• A：y=±2x
• B：
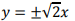
• C：
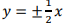
• D：

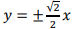
答 案：A

解 析：可以判断该曲线为双曲线且方程为y²-4x²=1，由y²-4x²=0得y=±2x即为所求渐近线方程。

2、甲、乙、丙、丁、戊五个学生排成一排，甲必须排在乙之前的不同排法为（）。

• A：
• B：
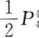
• C：
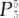
• D：

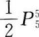
答 案：D

解 析：若不考虑甲必须排在乙前面的情况，共有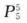种排法，其中，丙丁戊的排法位置相同，仅甲乙排列位置相反的排法各占一半，故甲排在乙前面的排法为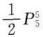。所以本题答案为D。

3、函数y=1+log2x(x>0)的反函数为（）。

• A：y=2^1-x(x∈R)
• B：y=2^x-1(x∈R)
• C：
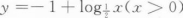
• D：

答 案：B

解 析：已知y=1+log₂x，则有log₂x=y-1，化简得x=2^y-1，故原函数的反函数为y=2^x-1(x∈R)。

4、已知点A(1，-3)，B(0，-3)，C(2，2)，则△ABC的面积为（）

• A：2
• B：3
• C：
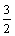
• D：

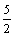
答 案：D

解 析：易知AB=1，点C到AB边的距离为2+3=5，故AB边的高为5，因此三角形的面积为.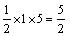

主观题

1、

答 案：

2、正四面体ABCD内接于半径为R的球，求正四面体的棱长。  

答 案：  

3、在锐角二面角α-l-β中，P∈α，A、B∈l，∠APB=90°，PA=2√3，PB=2√6，PB与β成30°角，求二面角α-l-β的大小。  

答 案：  

4、在△ABC中，A=30°，AB=，BC=1.(Ⅰ)求C；(Ⅱ)求△ABC的面积.

答 案：

填空题

1、己知球的一个小圆的面积为π，球心到小圆所在平面的距离为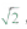，则这个球的表面积为_______

答 案：13π

2、设函数f(x)=x+b，且f(2)=3，则f(3)=______。

答 案：4

解 析：由题可知f(2)=2+6=3，得b=1，故f(3)=3+b=3+1=4.