课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(理)》每日一练试题05月16日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、过点(-2,2)与直线x+3y-5=0平行的直线是()
- A:x+3y-4=0
- B:3x+y+4=0
- C:x+3y+8=0
- D:3x-y+8=0
答 案:A
解 析:所求直线与x+3y-5=0平行,可设所求直线为x+3y+c=0,将点(一2,2)带入直线方程,故-2+3×2+c=0,解得c=-4,因此所求直线为线为x+3y-4=0.
2、设0
答 案:D
解 析: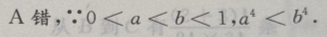
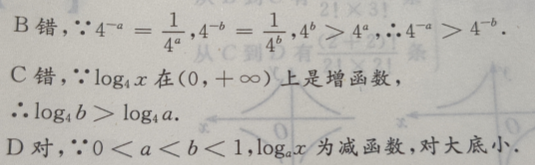
3、函数 的定义域为()。
的定义域为()。
- A:R
- B:{1}
- C:{x||x|≤1)
- D:{x||x|≥1}
答 案:A
解 析:本题主要考查的知识点为函数的定义域.
对于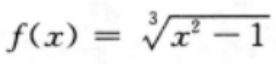 ,奇次根号下无要求,故函数的定义域为R
,奇次根号下无要求,故函数的定义域为R
4、设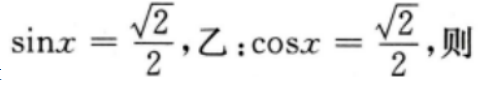 ()
()
- A:甲是乙的充分条件但不是必要条件
- B:甲是乙的必要条件但不是充分条件
- C:甲是乙的充要条件
- D:甲既不是乙的充分条件也不是乙的必要条件
答 案:D
解 析:本题主要考查的知识点为简易逻辑 由于 故甲既不是乙的充分条件,也不是乙的必要条件
故甲既不是乙的充分条件,也不是乙的必要条件
主观题
1、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:
答 案:(Ⅰ)由题意知(如图所示) 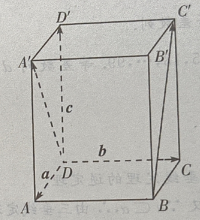
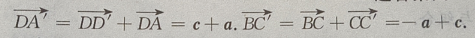
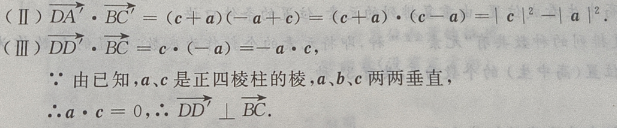
2、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 ,得
,得 设A(x1,y1),B(x2,y2),则
设A(x1,y1),B(x2,y2),则 因此
因此
3、已知函数f(x)=(x-4)(x2-a)
(I)求f"(x);
(Ⅱ)若f"(-1)=8,求f(x)在区间[0,4]的最大值与最小值
答 案: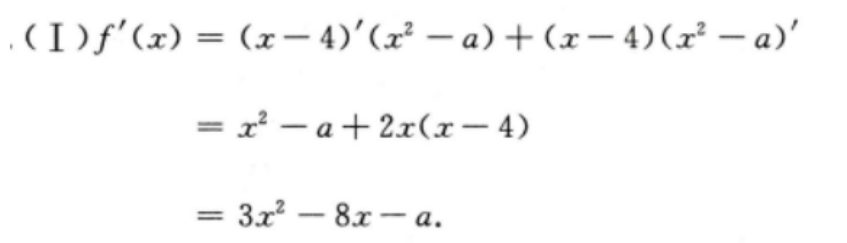

4、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。
(I)求C的方程;
(Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB
答 案:(I)由题意,该抛物线的焦点到准线的距离为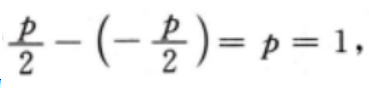 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得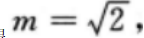 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为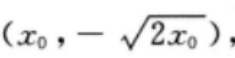 则
则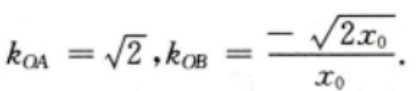 因为
因为 则有
则有 即
即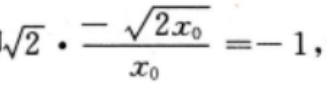 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
填空题
1、不等式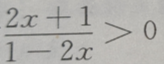 的解集为()
的解集为()
答 案: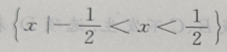
解 析:

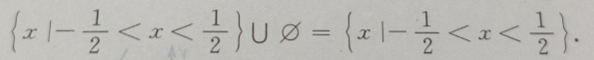
2、函数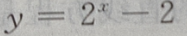 的图像与坐标轴的交点共有()
的图像与坐标轴的交点共有()
答 案:2
解 析:当x=0时,y=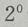 -2=-1,故函数与y轴交于(0,-1)点,令y=0,则有
-2=-1,故函数与y轴交于(0,-1)点,令y=0,则有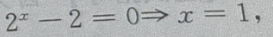 故函数与x轴交于(1,0) 点,因此函数
故函数与x轴交于(1,0) 点,因此函数 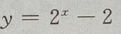 与坐标轴的交点共有 2个.
与坐标轴的交点共有 2个.
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!




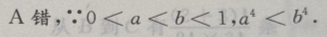
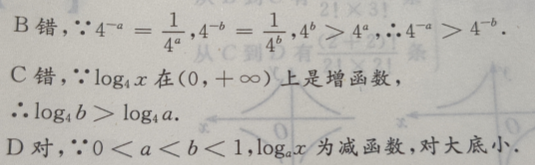
 的定义域为()。
的定义域为()。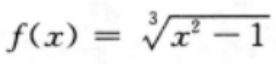 ,奇次根号下无要求,故函数的定义域为R
,奇次根号下无要求,故函数的定义域为R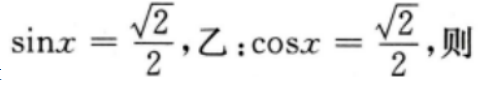 ()
() 故甲既不是乙的充分条件,也不是乙的必要条件
故甲既不是乙的充分条件,也不是乙的必要条件 (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:

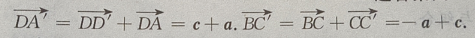
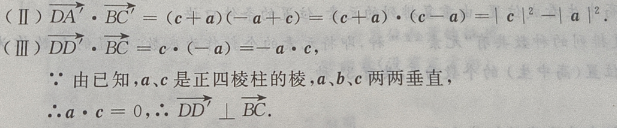
 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标; ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 ,得
,得 设A(x1,y1),B(x2,y2),则
设A(x1,y1),B(x2,y2),则 因此
因此
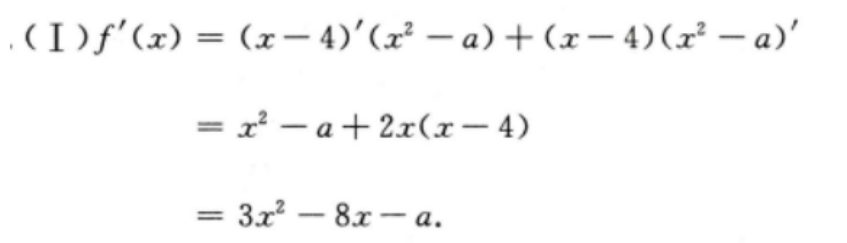

 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得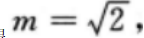 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为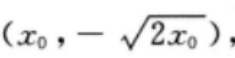 则
则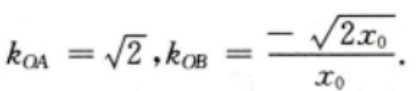 因为
因为 则有
则有 即
即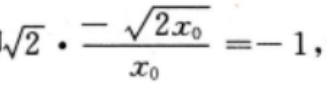 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
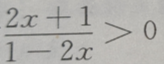 的解集为()
的解集为()
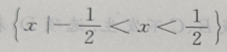


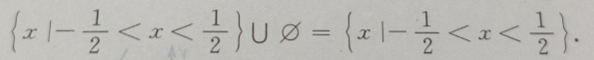
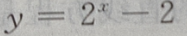 的图像与坐标轴的交点共有()
的图像与坐标轴的交点共有()
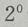 -2=-1,故函数与y轴交于(0,-1)点,令y=0,则有
-2=-1,故函数与y轴交于(0,-1)点,令y=0,则有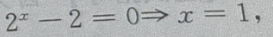 故函数与x轴交于(1,0) 点,因此函数
故函数与x轴交于(1,0) 点,因此函数 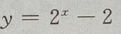 与坐标轴的交点共有 2个.
与坐标轴的交点共有 2个.


