2024年成考高起点《数学(文史)》每日一练试题05月14日
2024-05-14 12:08:02 来源:吉格考试网
2024年成考高起点《数学(文史)》每日一练试题05月14日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、下列函数为奇函数的是 ( )。
- A:

- B:
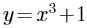
- C:

- D:
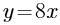
答 案:D
解 析:本题主要考查的知识点为函数的奇偶性. 【应试指导】f(z)=sinx=-sin(-x)=-f(-x),所以y=sinx为奇函数.
2、已知点M(-2,5),N(4,2),点P在 上,且
上,且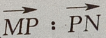 =1:2,则点P的坐标为()
=1:2,则点P的坐标为()
- A:
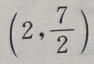
- B:(0,4)
- C:(8,2)
- D:(2,1)
答 案:B
解 析:由题意得: 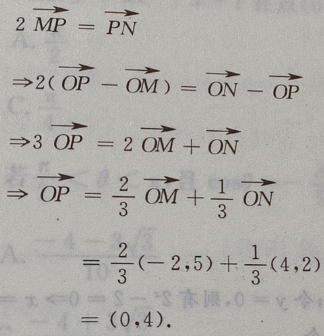
3、甲袋内有2个白球3个黑球,乙袋内有3个白球1个黑球,现从两个袋内各摸出1个球,摸出的两个球都是白球的概率是
- A:

- B:
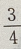
- C:

- D:
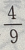
答 案:C
解 析:由已知条件可知此题属于相互独立同时发生的事件,从甲袋内摸到白球的概率为P(A)=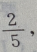 乙袋内摸到白球的概率为
乙袋内摸到白球的概率为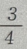 ,所以现从两袋中各提出一个球,摸出的两个都是白球的概率为
,所以现从两袋中各提出一个球,摸出的两个都是白球的概率为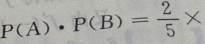
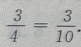
4、函数f(x)=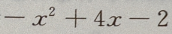 在区间[1,4]上的最大值和最小值分别是()
在区间[1,4]上的最大值和最小值分别是()
- A:2和-2
- B:2,没有最小值
- C:1和1
- D:2和4
答 案:A
解 析:f(x)=

主观题
1、在△ABC中,B=120°,C=30°,BC=4,求△ABC的面积.
答 案:因为A= 180°-B-C=30°,所以AB = BC=4.因此△ABC的面积
2、已知等差数列 前n项和
前n项和 (Ⅰ)求通项
(Ⅰ)求通项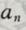 的表达式
(Ⅱ)求
的表达式
(Ⅱ)求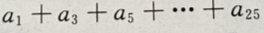 的值
的值
答 案:(Ⅰ)当n=1时,由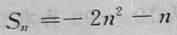 得
得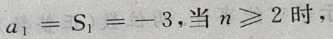
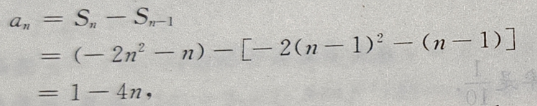
 也满足上式,故
也满足上式,故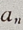 =1-4n(n≥1)
(Ⅱ)由于数列
=1-4n(n≥1)
(Ⅱ)由于数列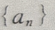 是首项为
是首项为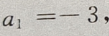 公差为d=-4的等差数列,所以
公差为d=-4的等差数列,所以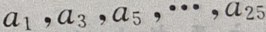 是首项为
是首项为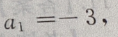 公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:
公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:

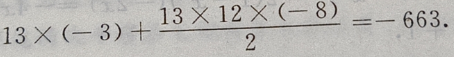
3、设椭圆的中心是坐标原点,长轴在x轴上,离心率 已知点P
已知点P 到圆上的点的最远距离是
到圆上的点的最远距离是 求椭圆的方程
求椭圆的方程
答 案:由题意,设椭圆方程为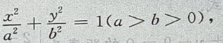 由
由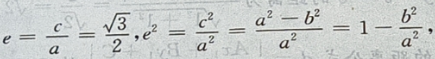
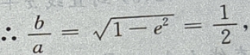 设P
设P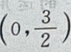 点到椭圆上任一点的距离为 d,
点到椭圆上任一点的距离为 d,
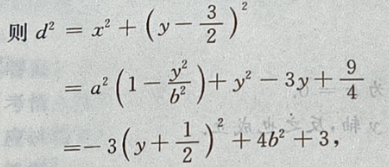
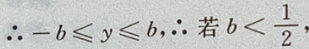 则在y=-b时,
则在y=-b时,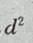 最大,即d也最大。
最大,即d也最大。
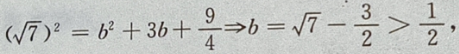

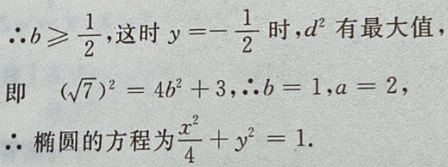
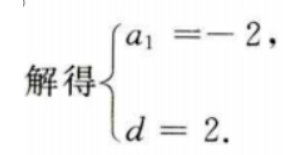
4、已知等差数列{an}中,a1+a3+a5=6,a2+a4+a6=12,求{an}的首项与公差.
答 案:因为{an}为等差数列,则
填空题
1、任选一个不大于20的正整数,它恰好是3的整数倍的概率是()
答 案: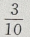
解 析:设n为不大于20的正整数的个数,则n=20,m为在这20个数中3的倍数:3,6、9、12、15、18的个数。 ∴m=6,∴所求概率=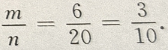
2、过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。
答 案: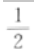
解 析:本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有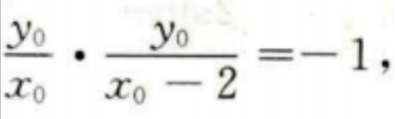 即
即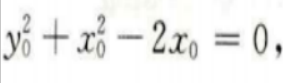
 所以
所以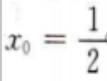 故切点横坐标为
故切点横坐标为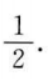
2023年成考高起点《数学(文史)》每日一练试题05月14日 05-14 2024年成考高起点《数学(文史)》每日一练试题05月05日 05-05 2024年成考高起点《数学(文史)》每日一练试题02月14日 02-14 2024年成考高起点《数学(文史)》每日一练试题01月14日 01-14 2024年成考高起点《数学(文史)》每日一练试题03月14日 03-14 2024年成考高起点《数学(文史)》每日一练试题04月14日 04-14 2024年成考高起点《数学(文史)》每日一练试题08月14日 08-14 2024年成考高起点《数学(文史)》每日一练试题07月14日 07-14



