2024年成考高起点《数学(理)》每日一练试题05月01日

2024年成考高起点《数学(理)》每日一练试题05月01日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、设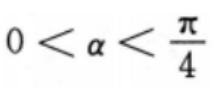，则 （）。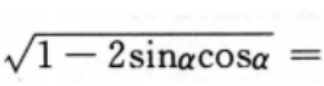

• A：sina+cosa
• B：—sing—cosa
• C：sing—coso
• D：cosa—sina

答 案：D

解 析：本题主要考查的知识点为三角函数的运算.当时，

2、在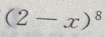的展开式中,的系数是

• A：448
• B：1140
• C：-1140
• D：-448

答 案：D

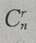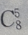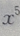解 析：直接套用二项式展开公式: 注:展开式中第r+1项的二项式系数与第r+1项的系数不同,此题不能只写出就为的系数  

3、袋中有6个球，其中4个红球，2个白球，从中随机取出2个球，则其中恰有1个红球的概率为（）

• A：
• B：
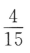
• C：
• D：

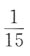
答 案：A

解 析：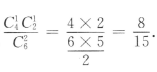

4、（ ）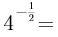

• A：-2
• B：
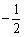
• C：
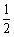
• D：2

答 案：C

主观题

1、已知等差数列｛an｝中，a1+a2+a3=6,a2+a4+a5= 12求｛an｝的首项与公差。  

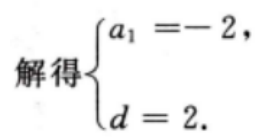
答 案：因为｛an｝为等差数列，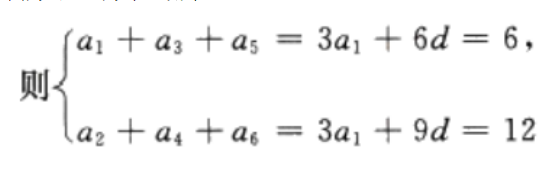

2、已知函数f(x)=(x-4)(x²-a) （I）求f"(x)； (Ⅱ)若f"(-1)=8，求f(x)在区间[0，4]的最大值与最小值

答 案：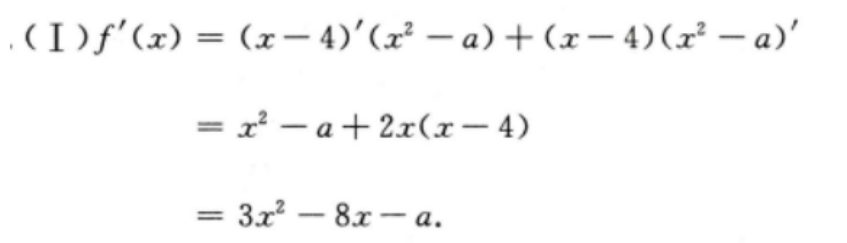

3、已知a,b,c成等差数列，a,b,c+1成等比数列．若b=6，求a和c．

答 案：由已知得解得

4、记△ABC的内角A，B，C的对边分别为a，b，c，已知B=60°，b²=ac，求A。    

答 案：由余弦定理b²=a²+c²-2accosB，可得ac=a²+c²-ac，即a²+c²-2ac=(a-c)²=0，解得a=c。 又因为B=60°，故△ABC为等边三角形，所以A=60°

填空题

1、椭圆的中心在原点，一个顶点和一个焦点分别是直线x+3y-6与两坐标轴的交点,则此椭圆的标准方程为（）  

答 案：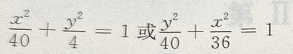

解 析：原直线方程可化为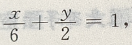交点(6,0),(0,2). 当点(6,0)是椭圆一个焦点,点(0,2) 是椭圆一个顶点时,c=6,b=2,当点(0,2) 是椭圆一个焦点,(6,0) 是椭圆一个顶点时,c=2,b-6,

2、不等式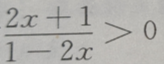的解集为（）  

答 案：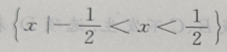

解 析：