2022年成考高起点《数学(理)》每日一练试题10月12日

2022年成考高起点《数学(理)》每日一练试题10月12日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知一次函数y＝2x＋b的图像经过点（-2，1），则该图像也经过点（　　）

• A：（1，7）
• B：（1，-3）
• C：（1，5）
• D：（1，-1）

答 案：A

解 析：因为一次函数了y＝2x＋b的图像过点（－2，1），所以，1＝2×（－2）＋b，b＝5，即y＝2x＋5．结合选项，当x＝1时，y＝7，故本题选A．

2、下列函数中，为奇函数的是（）

• A：
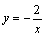
• B：y=-2x+3
• C：y=x^2-3
• D：y=3cosx

答 案：A

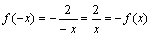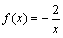解 析：对于A选项，，故是奇函数.

3、圆x2+y2+2x-6y-6=0的半径为()。

• A：
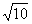
• B：4
• C：
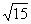
• D：16

答 案：B

解 析：本题考查了圆的方程的知识点。   圆x²+y²+2x﹣6y﹣6=0可化为(x+1)²+(y-3)²=16，故圆的半径为4。

4、已知函数f(x)的定义域为R，且f(2x)=4x+1，则f(1)=（）

• A：9
• B：5
• C：7
• D：3

答 案：D

解 析：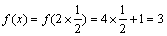

主观题

1、已知a、b、c成等比数列，x是a、b的等差中项，y是b、c的等差中项，证明a/x+c/y=2。

答 案：由已知条件得，b2=ac，2x=a+b，2y=b+c①∴2cx=ac+bc，2ay=ab+ac。②②中两式相加得，2ay+2cx=ab+2ac+bc，又①中后两式相乘得，4xy=(a+b)(b+c)=ab+2ac+bc；
∴2ay+2cx=4xy，a/x+c/y=2。

2、在△ABC中，BC=a，AC=b，a，b是方程的两个根，且2cos(A+B)=1.求：
（Ⅰ）角C的度数。
（Ⅱ）AB的长度。

答 案：（Ⅰ）cosC=cos[π-(A+B)]=-cos(A+B)=-1/2，所以，C=120°。（Ⅱ）由题意可知，a+b=2√3，ab=2，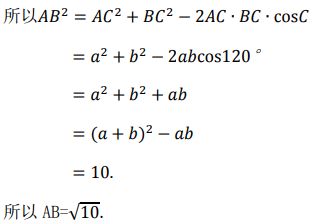

3、

答 案：

4、

答 案：

填空题

1、从一个正方体中截去四个三棱锥，得一正三棱锥ABCD，正三棱锥的体积是正方体体积的(  )。

答 案：1/3

解 析：截去的四个三棱锥的体积相等，其中任一个三棱锥都是底面为直角三角形,且直角边长与这个三棱锥的高相等，都等于正方体的棱长．设正方体的棱长为a，则截去的一个三棱锥的体积为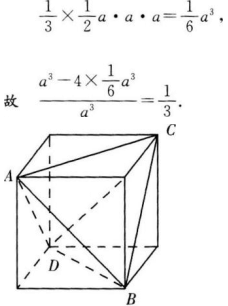

2、函数f(x)=x2+bx+c的图像经过点(-1，0)，（3，0)，则f(x)的最小值为______。

答 案：-4

解 析：由于函数开口向上，故其在对称轴处取得最小值，又函数过点(-1，0)，(3，0)，故其对称轴为x=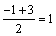，f_min(1)=1+b+C，而f(-1)由1-b+c=0，f(3)=9+3b+c=0，得b=-2，c=-3，故f_min（1)=1-2-3=-4.