课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2022年成考高起点《数学(文史)》每日一练试题10月07日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、某学校为新生开设了4门选修课程,规定每位新生至少要选其中3门,则一位新生不同的选课方案共有 ( )
答 案:C
2、函数:y=log2(x+2)的图像向上平移1个单位后,所得图像对应的函数为()。
- A:y=log2(x+1)
- B:y=log2(x+3)
- C:y=log2(x+2)-1
- D:y=log2(x+2)+1
答 案:D
解 析:本题考查了函数图像的平移的知识点。
函数y=log2(x+2)的图像向上平移1个单位后,所得图像对应的函数为y-1=log2(x-0+2),即y=log2(x+2)+1。
3、如果一次函数y=kx+b的图像经过点A(1,7)和B(0,2),则k=
答 案:D
4、从1,2,3,4,5中任取3个数,组成的没有重复数字的三位数共有 ( )
答 案:D
解 析:本题主要考查的知识点为排列组合.【应试指导】此题与顺序有关,所组成的没有重复
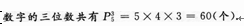
主观题
1、已知数列 {an}中,Sn是它的前n项和,并且 Sn+1=4an+2,a1=1。(Ⅰ)设 bn=an+1−2an,求证:数列{bn}是等比数列;
(Ⅱ)设 cn=an/2n,求证:数列{cn}是等差数列;
(Ⅲ)求数列{an}的通项公式及前n项和。
答 案:
2、设ƒ(x)=ax-1,其中常数a>0,如果{xn}是等差数列,且xn=2n-1,
(Ⅰ)求证:{ƒ(xn)}是等比数列;
(Ⅱ)求数列{ƒ(xn)}的前n项和Sn的表达式。
答 案:
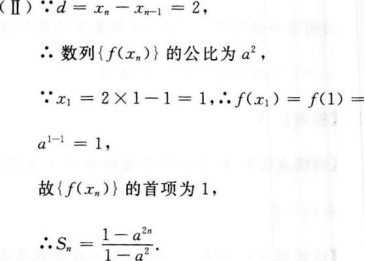
3、每亩地种果树20棵时,每棵果树收入90元,如果每亩增种一棵,每棵果树收入就下降3元,求使总收入最大的种植棵数。
答 案:设每亩增种x棵,总收人为y元,则每亩种树(20+x)棵,由题意知增种z棵后每棵收入为(90-3x)元,则有y=(90-3x)(20+x),整理得y=-3x2+30x+1800,配方得y=-3(x-5)2+1875,当x=5时,y有最大值,所以每亩地最多种25棵。
4、问数列:lg100,lg(100sin45°),lg(100sin245°),…,lg(100sinn-145°)前几项和最大?并求最大值.(lg2=0.3010)
答 案:
填空题
1、过点(1,-2)且与直线3x+y-1=0垂直的直线方程为_______。
答 案:x-3y-7=0
解 析:本题考查了直线方程的知识点。
因为所求直线与直线3x+y-1=0垂直,故可设所求直线方程为x-3y+a=0;又直线经过点(1,-2),故1-3×(-2)+a=0,则a=-7,即所求直线方程为x-3y-7=0。
2、已知曲线y=lnx+a在点(1,a)处的切线过点(2,-1),则a=______。
答 案:-2
解 析: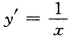 ,故曲线在点(1,a)处的切线的斜率为
,故曲线在点(1,a)处的切线的斜率为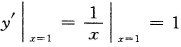 ,因此切线方程为:y-a=x-1,即y=x-1+a,又切线过点(2,-1),因此有-1=2-1+a,故a=-2.
,因此切线方程为:y-a=x-1,即y=x-1+a,又切线过点(2,-1),因此有-1=2-1+a,故a=-2.
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
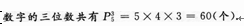


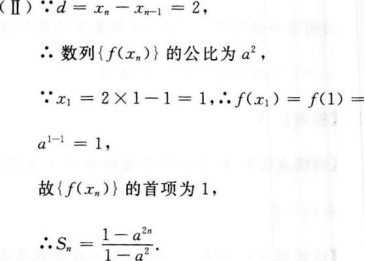

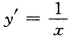 ,故曲线在点(1,a)处的切线的斜率为
,故曲线在点(1,a)处的切线的斜率为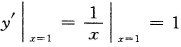 ,因此切线方程为:y-a=x-1,即y=x-1+a,又切线过点(2,-1),因此有-1=2-1+a,故a=-2.
,因此切线方程为:y-a=x-1,即y=x-1+a,又切线过点(2,-1),因此有-1=2-1+a,故a=-2.


