2022年成考高起点《数学(文史)》每日一练试题09月19日
2022-09-19 11:29:09 来源：吉格考试网
2022年成考高起点《数学(文史)》每日一练试题09月19日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。
单选题
1、某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共有 ( )
- A：7种
- B：4种
- C：5种
- D：6种
答 案：C
2、已知cos2a=5/13(3π/2＜a＜2π)，则tanα等于（）。
- A：
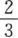
- B：
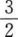
- C：
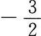
- D：
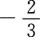
答 案：D
解 析：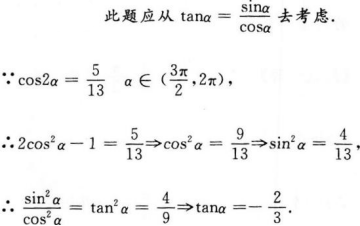
3、已知直线L与直线2x-3y+5=0平行，则L的斜率为（）。
- A：
- B：
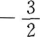
- C：
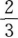
- D：
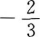
答 案：C
解 析：已知直线L与直线2x-3y+5=0平行，所以K=2/3。
4、当a=1时，函数ƒ(x)=2ax2+(a-1)x+3的对称轴方程为（）。
- A：x=0
- B：y=0
- C：x=1/2
- D：x=3
答 案：A
解 析：当a=1时，ƒ(x)=2x2+3，此时抛物线的对称轴方程为x=0。
主观题
1、求(I)AB;
答 案：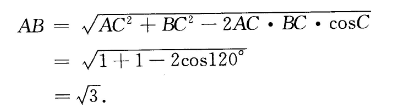
2、已知椭圆E的中心在坐标原点O，焦点在x轴上，长轴长为8，焦距为
.(Ⅰ)求E的标准方程；(Ⅱ)若以O为圆心的圆与E交于四点，且这四点为一个正方形的四个顶点，求该圆的半径.
答 案：
3、在△ABC中，AB=2,BC=3,B=60°，求AC及△ABC的面积。
答 案：根据余弦定理得出
4、
答 案：
填空题
1、从5位男生和4位女生中选出2人作代表，恰好一男生和一女生的概率是（）。
答 案：5/9
解 析：从5位男生和4位女生中任选2人的选法共有
种，恰好一男生和一女生的选法共有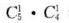
种，所以恰好选出一男生和一女生的概率是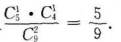
2、已知曲线y=lnx+a在点(1，a)处的切线过点(2，-1)，则a=______。
答 案：-2
解 析：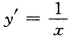
，故曲线在点(1，a)处的切线的斜率为
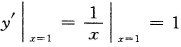，因此切线方程为：y-a=x-1，即y=x-1+a，又切线过点(2，-1)，因此有-1=2-1+a，故a=-2.
2023年成考高起点《数学(文史)》每日一练试题09月19日 09-19 2024年成考高起点《数学(文史)》每日一练试题09月19日 09-19 2022年成考高起点《数学(文史)》每日一练试题10月19日 10-19 2022年成考高起点《数学(文史)》每日一练试题12月19日 12-19 2022年成考高起点《数学(文史)》每日一练试题07月19日 07-19 2022年成考高起点《数学(文史)》每日一练试题11月19日 11-19 2022年成考高起点《数学(文史)》每日一练试题09月09日 09-09 2022年成考高起点《数学(文史)》每日一练试题07月09日 07-09
- 备考交流
-
2024成考内部交流群群号：665429327
扫一扫或点击二维码入群
