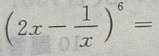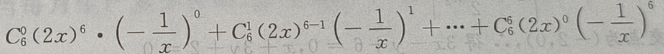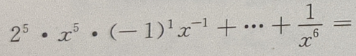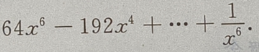2023年成考高起点《数学(理)》每日一练试题12月16日

2023年成考高起点《数学(理)》每日一练试题12月16日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知向量a=(3,4),向量 b=(0,-2),则cos的值为（）

• A：
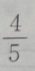
• B：
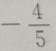
• C：
• D：

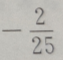
答 案：B

解 析：求cos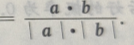可直接用公式cos a·b=(3,4)·(0,-2)=3×0+4×(-2)=8,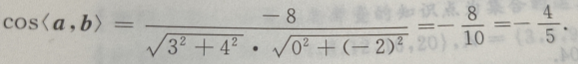  

2、若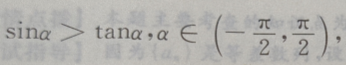则（）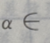

• A：
• B：
• C：
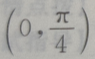
• D：

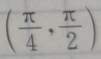
答 案：B

解 析：首先做出单位圆,然后根据问题的约束条件,利用三角函数线找出满足条件的a角取值范围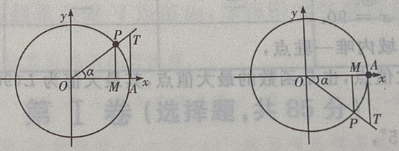  

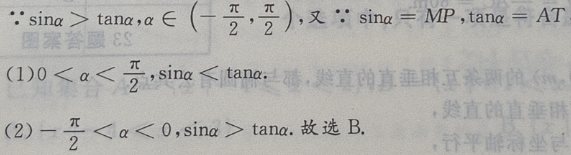
3、给出下列两个命题：①如果一条直线与一个平面垂直，则该直线与该平面内的任意一条直线垂直②以二面角的棱上任意一点为端点，在二面角的两个面内分别作射线，则这两条射线所成的角为该二面角的平面角.则（）

• A：①②都为真命题
• B：①为真命题，②为假命题
• C：①为假命题，②为真命题
• D：①②都为假命题

答 案：B

解 析：一条直线与平面垂直，则直线与平面内的任意一条直线垂直，故①为真命题；二面角的两条射线必须垂直于二面角的棱，故②为假命题，因此选B选项．

4、函数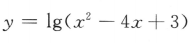的定义域是（）

• A：{x|-3＜x＜-1}
• B：{x|x＜-3或x＞-1}
• C：{x|1＜x＜3}
• D：{x|x＜1或x＞3}

答 案：D

解 析：由对数函数的性质可知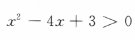，解得x＞3或x＜1，因此函数的定义域为{x|x＜1或x＞3}

主观题

1、在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量和关于基底{a,b,c}的分解式; （Ⅱ）求证： （Ⅲ）求证：  

答 案：（Ⅰ）由题意知(如图所示)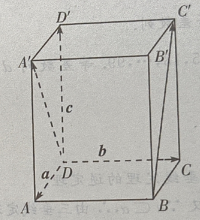  

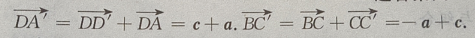
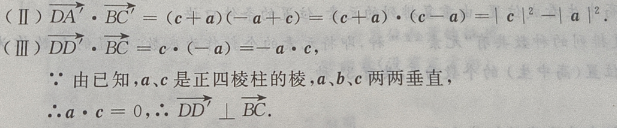
2、在正四棱柱ABCD-A'B'C'D'中， （Ⅰ）写出向量关于基底{a,b,c}的分解式 （Ⅱ）求证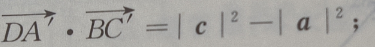： （Ⅲ）求证：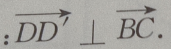  

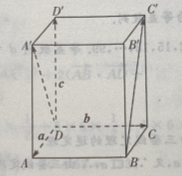
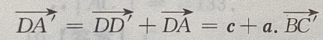
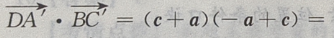
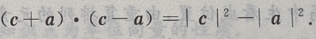答 案：(Ⅰ)由题意知(如图所示) (Ⅱ) (Ⅲ)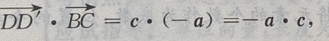 由已知，a,c是正四棱柱的棱，a,b,c两两垂直  

3、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得AB=120m,求河的宽

答 案：如图， ∵∠C=180°-30°-75°=75° ∴△ABC为等腰三角形，则AC=AB=120m 过C做CD⊥AB,则由Rt△ACD可求得CD==60m， 即河宽为60m  

4、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由，得设A（x1,y1），B（x2,y2），则因此

填空题

1、若平面向量a=(x,1),b=(1,-2),且a//b,则x=（）  

答 案：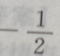

解 析：由于a//b，故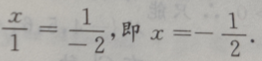

2、的展开式是（）

答 案：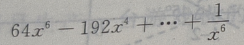

解 析：