2022年成考高起点《数学(理)》每日一练试题09月12日

2022年成考高起点《数学(理)》每日一练试题09月12日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、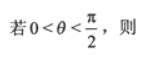

• A：
• B：
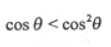
• C：
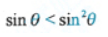
• D：

答 案：D

2、从A、B两个不同的队中选出选手参加比赛，A队有5名选手，B队有4名选手，从A中选出3名选手，B中选出2名选手，则不同的选法有（）。

• A：60种
• B：72种
• C：120种
• D：240种

答 案：A

解 析：从A队5名选手中选出2名选手共有种情况，从B队4名选手中选出2名选手共有种情况，由分步乘法原理可得共种选法。

3、已知三角形的两个顶点是椭圆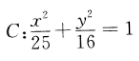的两个焦点，第三个顶点在C上，则该三角形的周长为（）。

• A：10
• B：20
• C：16
• D：26

答 案：C

解 析：该小题主要考查的知识点为椭圆的性质. 【考试指导】

4、根据连续函数的定义，下列函数在指定点或开区间上不连续的是（）

• A：ƒ(x)=2x+1，点x=-1
• B：ƒ(x)=ax^{2+bx+C，点x=0}
• C：
• D：

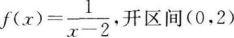
答 案：C

主观题

1、

答 案：

2、

答 案：

3、已知{an}为等差数列，且a3=a5+1. (Ⅰ)求{an}的公差d； (Ⅱ)若a1=2，求{an}的前20项和S20.

答 案：(Ⅰ)设公差为d，知a₅=a+₃2d， 故a₅=a₃+2d=a₃-1， 因此有d=-1/2. (Ⅱ)由前n项和公式可得

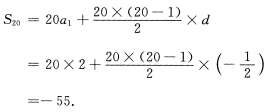
4、等差数列{a_n}中，a₁=-393，a₂+a₃=-768，{b_n}是等比数列，q∈(0,1)，b1=2，{b_n}的前n项和为20，求：（Ⅰ）求a_n，b_n；
（Ⅱ）解不等式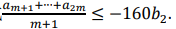

答 案：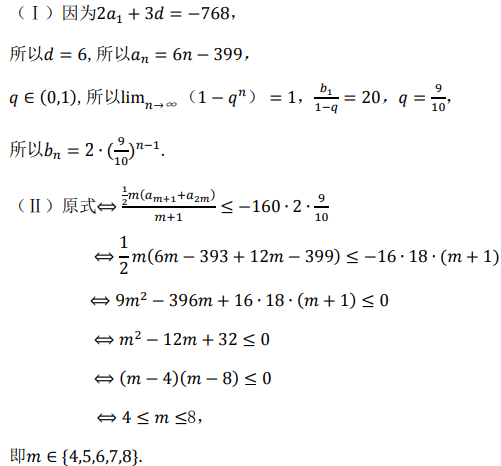

填空题

1、不等式|x—1|<1的解集为___.

答 案：{x|0

解 析：该小题主要考查的知识点为不等式的解集. |x -1|<1=>-10

2、曲线y=x2-ex+1在点(0，0)处的切线方程为___________________。

答 案：x+y=0  

解 析：本题考查了导数的几何意义的知识点。 根据导数的几何意义，曲线在(0，0)处的切线斜率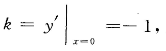，则切线方程为y-0=-1·(x-0)，化简得：x+y=0。