2022年成考高起点《数学(理)》每日一练试题09月06日

2022年成考高起点《数学(理)》每日一练试题09月06日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、过点(0，1)且与直线x+y+1=0垂直的直线方程为( )

• A：y=x+1
• B：y=2x+1
• C：y=x
• D：y=x-1

答 案：A

解 析：与直线x+y+1=0垂直的斜率是1,并且该直线同时过点(0,1)，所以该直线的方程应该为y-1=1*(x-0)，即y=x+1,答案为：A

2、某学校为新生开设了4门选修课程，规定每位新生至少要选其中3门，则一位新生不同的选课方案共（）。

• A：7种
• B：4种
• C：5种
• D：6种

答 案：C

解 析：该小题主要考查的知识点为组合数.【考试指导】由题意知，新生可选3门或4门选修课程，则不同的选法共有:

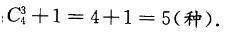
3、若等比数列{an}的公比为3，a4=9，则a1=

• A：27
• B：1/9
• C：1/3
• D：3

答 案：C

4、若tanα=3，则tan(α+π/4)=（）。

• A：-2
• B：1/2
• C：2
• D：-4

答 案：A

解 析：该小题主要考查的知识点为三角函数的运算.

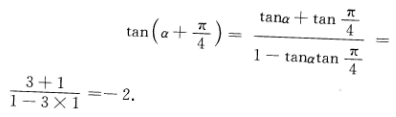
主观题

1、

答 案：

2、设椭圆的焦点为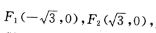其轴长为4(Ⅰ)求椭圆的方程；(Ⅱ)设直线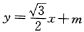与椭圆有两个不同的交点，其中一个交点的坐标是（0,1），求另一个交点的坐标。

答 案：

3、建筑一个容积为8000m³，深为6m的长方体蓄水池，池壁每m2的造价为15元，池底每m2的造价为30元。(Ⅰ)把总造价y(元)表示为长x(m)的函数；
(Ⅱ)求函数的定义域。

答 案：

4、已知a、b、c成等比数列，x是a、b的等差中项，y是b、c的等差中项，证明a/x+c/y=2。

答 案：由已知条件得，b2=ac，2x=a+b，2y=b+c①∴2cx=ac+bc，2ay=ab+ac。②②中两式相加得，2ay+2cx=ab+2ac+bc，又①中后两式相乘得，4xy=(a+b)(b+c)=ab+2ac+bc；
∴2ay+2cx=4xy，a/x+c/y=2。

填空题

1、方程Ax2+Ay2+Dx+Ey+F=0(A≠0)满足条件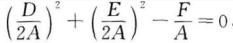，它的图像是（）。

答 案：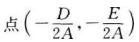

2、设球的表面积为4π，则该球的体积为（）。

答 案：4π/3

解 析：