课程
题库
分享到空间
分享到新浪微博
分享到QQ
分享到微信

2024年成考高起点《数学(理)》每日一练试题12月23日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过成考高起点每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、若f(x)为偶函数,且在(0,+∞)为增函数,则下列不等式成立的是()。
答 案:B
解 析: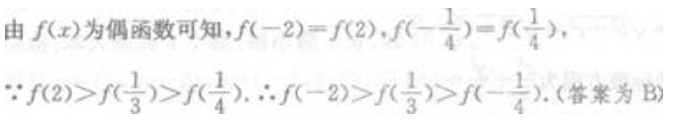
2、下列函数中,为奇函数的是()
答 案:B
解 析:当f(-x)=-f(x),函数f(x)是奇函数,只有选项B符合.
3、在△ABC中,已知a=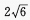 ,b=
,b=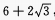 ,c=
,c=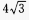 ,则()。
,则()。
- A:∠A<∠B<∠C
- B:∠A>∠B>∠C
- C:∠A<∠C<∠B
- D:∠A>∠C>∠B
答 案:C
解 析:由已知a=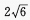 ,b=
,b=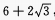 ,c=
,c=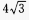 可知a
可知a
4、设f(x)是以7为周期的偶函数,且f(-2)=5,则f(9)=()。
答 案:B
解 析:因为f(x)是偶函数,所以f(2)=f(-2)=5,又因为f(x)是以7为周期的函数,则f(9)=f(7+2)=f(2)=5。答案为B。
主观题
1、已知a,b,c成等差数列,a,b,c+1成等比数列.若b=6,求a和c.
答 案:由已知得 解得
解得
2、已知数列{an}中,a1=2,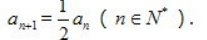 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
答 案:解:
3、空间有四个点,如果其中任何三点不在同一直线上,可以确定几个平面?
答 案:根据公理,在所给定的四点中任取三点,可确定一个平面,由组合公式 所以共可确定四个平面。
所以共可确定四个平面。
解 析:空间有n个点,如果其中任何三点不在同一直线上,可以确定 个平面。
个平面。
4、设A1A2A3A4A5A6为正六边形,如图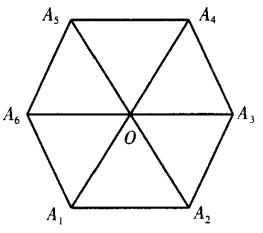 ,O为它的中心。 (1)求证:
,O为它的中心。 (1)求证: 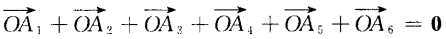 (2)
(2)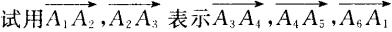
答 案:已知A1A2A3A4A5A6 为正六边形,即|A1A2|=|A3A4|=......|A6A1|.要证6个向量的和为0.只需证其中3个向量与另3个向量的长度相等、方向相反即可.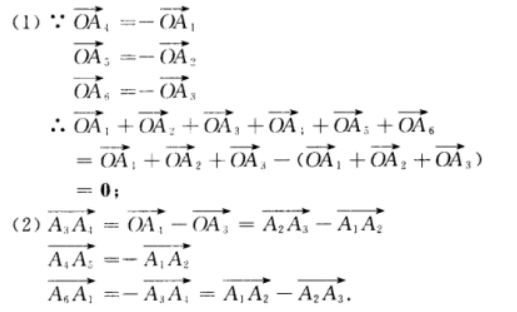
填空题
1、长方体的长、宽、高分别为2,3,6,则该长方体的对角线长为()
答 案:7
解 析:由题可知长方体的底面的对角线长为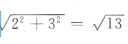 ,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为
,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为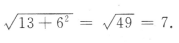
2、y=ax2-bx+c的导数y'|x=1=______。
答 案:2a-b
温馨提示:因考试政策、内容不断变化与调整,本站提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!
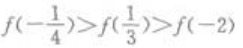
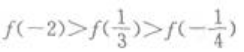
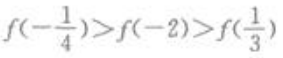
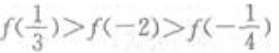
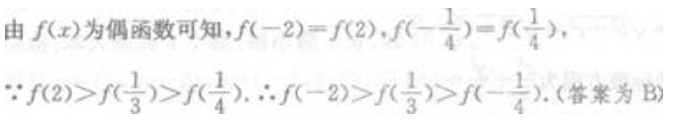
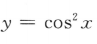
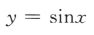
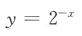
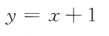
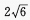 ,b=
,b=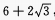 ,c=
,c=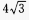 ,则()。
,则()。 解得
解得
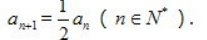 (Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{an}前5项的和 S5
 所以共可确定四个平面。
所以共可确定四个平面。 个平面。
个平面。
 ,O为它的中心。 (1)求证:
,O为它的中心。 (1)求证: 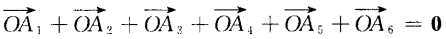 (2)
(2)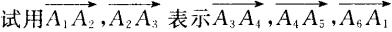
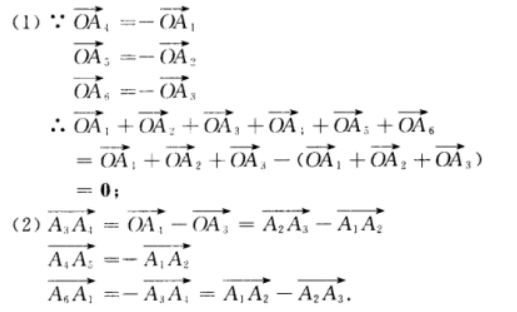
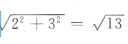 ,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为
,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为