2024年成考高起点《数学(文史)》每日一练试题12月21日

2024年成考高起点《数学(文史)》每日一练试题12月21日，可以帮助我们积累知识点和做题经验，进而提升做题速度。通过成考高起点每日一练的积累，助力我们更容易取得最后的成功。

单选题

1、已知f(x)=ax²+b的图像经过点（1,2）且其反函数f^-1（x）图像经过点（3,0），则函数f（x）的解析式是（）。

• A：
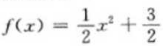
• B：f(x)=-x²+3
• C：f(x)=3x²+2
• D：f(x)=x²+3

答 案：B

解 析：∵f(x)的反函数f^-1（x）过点（3,0），所以f(x)又过点（3,0），所以有f（1）=2，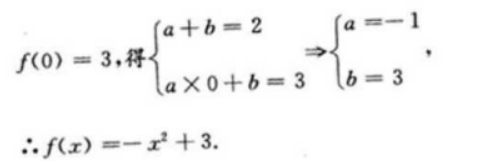

2、已知M为椭圆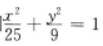上的一点，F₁,F₂是椭圆的两个焦点，且∠F₁MF₂=60°，则△F₁MF₂的面积为（）

• A：
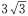
• B：3
• C：
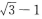
• D：

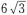
答 案：A

解 析：由椭圆方程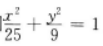 知，长轴长2a=10，焦距2c=8，设|MF1|=t，由余弦定理8²=t²+（10-t）²-2t（10-t）cos60°，得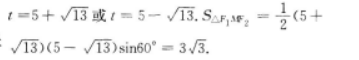

3、若函数y=f(x)在[-1,1]上是单调函数,则使得y=f(sinx)必为单调函数的区间是()  

• A：R
• B：[-1,1]
• C：
• D：[-sin1 ,sin1]

答 案：C

解 析：y=f(x)在[-1,1]上是单调函数,所以y=f(x)的单调区间为[-1,1]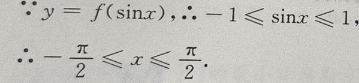  

4、若|a|=1，|b|=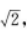（a-b）⊥a，则a与b的夹角为（　）

• A：30°
• B：45°
• C：60°
• D：75°

答 案：B

解 析：因为(a-b)⊥a， 【考点指要】本题考查向量的模与夹角的计算、向量的数量积的几何意义及对垂直问题的应用

主观题

1、求函数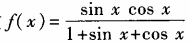（x∈R）的最大值与最小值。  

答 案：设sinx+cosx=t，则（sinx+cosx）²=t²，1+2sinxcosx=t²，sinxcosx= 于是转化为求的最值。 由所设知 上为增函数，故g（t）的最大值为最小值为

2、如图9-4，已知测速站P到公路L的距离为40米，一辆汽车在公路L上行驶，测得此车从A点行驶到8点所用的时间为2秒，并测得∠APO=60°，∠BPO=30°，计算此车从A到B的平均速度为多少km/h（结果保留到个位），并判断此车是否超过了80km/h的限制速度。

答 案：此车从A到B的平均速度为83（km/h），已经超过80km/h的限制速度。

3、已知a^m=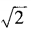，aⁿ=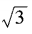，求a^3n-4m的值。  

答 案：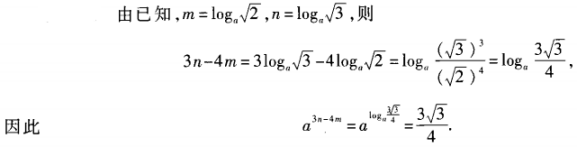

4、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

填空题

1、与已知直线7x+24y-5=0平行，且距离等于3的直线方程是______。  

答 案：7x+24y+70=0或7x+24y-80=0

解 析：设要求的直线方程为7x+24y+c=0， ∵直线7x+24y+c=0到直线7x+24y-5=0的距离等于3 ∴ ∴.C=70或-80. 故所求的直线方程为7x+24y+70=0或7x+24y-80=0

2、某人投篮每次命中率为0.8，现独立投篮4次，恰好命中3次的概率是______。  

答 案：0.4096

解 析：本题试验属于独立重复试验，其概率为