2024年高职单招《数学(中职)》每日一练试题09月10日,可以帮助我们积累知识点和做题经验,进而提升做题速度。通过高职单招每日一练的积累,助力我们更容易取得最后的成功。
单选题
1、“x为有理数”是“x2为有理数”的()
- A:充分不必要条件
- B:必要不充分条件
- C:充要条件
- D:既不充分也不必要条件
答 案:A
解 析:x为有理数,则x2一定为有理数,但x2为有理数,x不一定为有理数,比如3为有理数,但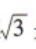 是无理数,所以“x为有理数”是“x2为有理数”的充分不必要条件.
是无理数,所以“x为有理数”是“x2为有理数”的充分不必要条件.
2、“a2>0”是“a>0”的()
- A:充分条件
- B:必要条件
- C:充要条件
- D:既不充分也不必要条件
答 案:B
解 析:由a2>0得a>0或a<0,所以“a2>0”是“a>0”的必要条件.
3、已知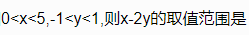 ()
()
- A:(2,3)
- B:(-2,3)
- C:(2,7)
- D:(-2,7)
答 案:D
解 析:因为-1
4、已知集合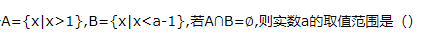
答 案:B
解 析: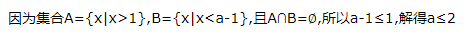
填空题
1、满足M∪{1}={0.1.2}的集合M的个数为()
答 案:2
解 析:因为M∪{1}={0,1,2},所以0,2必须是集合M中的元素,1可以是集合M中的元素,也可以不是集合M中的元素,所以M={0,2}或M={0,1,2},所以满足题意的M的个数是2.
2、已知集合A={x|x<2a-1},B={x|x≥1},且A∪B=R,则实数a的取值范围是()
答 案:a≥1
解 析:由A∪B=R,A={x|x<2a-1},B={x|x≥1}得2a-1≥1,解得a≥1.
3、已知集合A={1.2.3},B={a,3.4}.若A∩B={2,3},则a=()
答 案:2
解 析:∵A∩B={2,3},所以2∈B,又B={a,3,4},∴a=2.
4、已知集合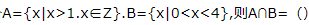
答 案:{2,3}
解 析:因为A={x|x>1,x∈Z}={2,3,4,…},B={x|0
简答题
1、已知m∈R,命题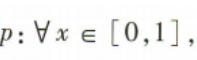 不等式m2-3m≤x2-2x-1恒成立.若p为真命题,求实数m的取值范围.
不等式m2-3m≤x2-2x-1恒成立.若p为真命题,求实数m的取值范围.
答 案:若命题p为真命题,则m2-3m≤(x2-2x-1)min, 因为x∈[0,1],
所以(x2-2x-1)min=-2,
所以m2-3m≤-2,解得1≤m≤2,所以m的取值范围为[1,2]
2、已知命题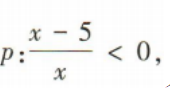 命题q:y=log2(x2-x-12)有意义.若p∧q为真命题,求实数x的取值范围.
命题q:y=log2(x2-x-12)有意义.若p∧q为真命题,求实数x的取值范围.
答 案:由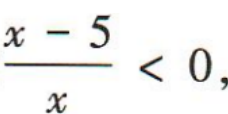 得02(x2-x-12)有意义,须x2-x-12>0,解得x<-3或x>4,即q:x<-3或x>4.因为p∧q为真,所以
得02(x2-x-12)有意义,须x2-x-12>0,解得x<-3或x>4,即q:x<-3或x>4.因为p∧q为真,所以 解得4
解得4
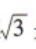 是无理数,所以“x为有理数”是“x2为有理数”的充分不必要条件.
是无理数,所以“x为有理数”是“x2为有理数”的充分不必要条件.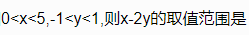 ()
() 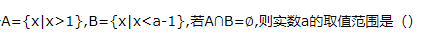
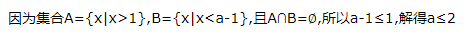
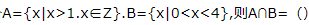
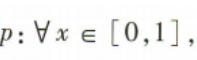 不等式m2-3m≤x2-2x-1恒成立.若p为真命题,求实数m的取值范围.
不等式m2-3m≤x2-2x-1恒成立.若p为真命题,求实数m的取值范围.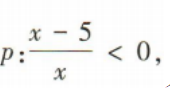 命题q:y=log2(x2-x-12)有意义.若p∧q为真命题,求实数x的取值范围.
命题q:y=log2(x2-x-12)有意义.若p∧q为真命题,求实数x的取值范围.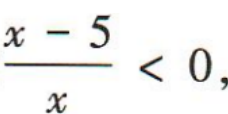 得0
得0 解得4
解得4


